Metodo Para Determinar La Velocidad de la Luz:Metodo de Fizeau
Determinación de la Velocidad de la Luz- Método Fizeau
 La luz avanza tan aprisa que nada en nuestra experiencia cotidiana nos conduce a pensar que su velocidad no sea infinita.
La luz avanza tan aprisa que nada en nuestra experiencia cotidiana nos conduce a pensar que su velocidad no sea infinita.
Se: requiere una considerable penetración inclusive para preguntar “Con qué rapidez se mueve la luz?”.
Galileo se hizo esta pregunta y trató de contestarla experimentalmente.
Su obra principal, Dos Nuevas Ciencias, publicada en Holanda en 1638, esté escrita en forma de una conversación entre tres personajes ficticios llamados Salviati, Sagredo y Simplicio.
Reproducimos una parte de lo que decían acerca de la velocidad de la luz.
Simplicio: La experiencia cotidiana nos muestra que la propagación de la luz es instantánea; porque cuando vemos que se dispara un cañón a distancia, el fogonazo llega a nuestros ojos sin que transcurra ningún tempo mientras que el sonido llega a nuestros oídos sólo después de un intervalo perceptible.
Sagredo: Bien, Simplicio, lo único que yo puedo inferir de esta experiencia tan común es que el sonido al llegar a nuestros oídos viaja más lentamente que la luz; no me informa si la llegada de la luz es instantánea o si, cuando sea sumamente rápida, de todas maneras invierte algún tiempo..
Sagredo: quien evidentemente es Galileo mismo, describe entonces un método posible para medir la velocidad de la luz.
El ayudante se colocan frente a frente separados alguna distancia la noche. Cada uno de ellos lleva una linterna que puede tapar destapar a voluntad. Galileo comenzó el experimento descubrí su linterna.
Cuando la luz le llegó al ayudante éste destapó su propia linterna, cuya luz fue vista por Galileo.
Cuando trató de medir tiempo transcurrido desde que él descubrió su propia linterna hastaa que le llegó la luz de la linterna de su ayudante. Actualmente sabemos que para una distancia de 1609 m (una milla) el tiempo para el viaje de ida y vuelta sería solamente de 11 X 10-8.
Este tiempo es mucho menor que los tiempos de reacción humana de modo que el método falla.
Para medir una gran velocidad directamente, o bien medimos un Intervalo de tiempo pequeño o bien usamos una línea de base grande.
Esta situación sugiere que la astronomía, que trata con grandes distancias, podría ser capaz de dar un valor experimental para la velocidad de la luz; efectivamente así fue.
Aun cuando sería deseable medir el tiempo que tarda la luz del Sol en llegar a la Tierra, no hay manera de saber cuándo sale del Sol la luz que nos llega en un instante dado; debemos usar métodos astronómicos más elaborados.
Sin embargo, nótese que las señales de radar son reflejadas con toda regularidad por la Luna; esto nos da una línea de base de 7.68 X 108 m (de ida y vuelta) para medición de tiempo.
La velocidad de la luz (y de las microondas) es tan bien conocida en la actualidad mediante otros experimentos que estas mediciones se usan para determinar exactamente la distancia a la Luna.
También se han podido obtener reflexiones de señales de microondas desde Venus.
 En 1675 Roemer (imagen izq.), un astrónomo danés que observaba en Paris, hizo algunas observaciones de los satélites de Júpiter de las cuales se puede deducir una velocidad de la luz de 2 X 108 m/seg.
En 1675 Roemer (imagen izq.), un astrónomo danés que observaba en Paris, hizo algunas observaciones de los satélites de Júpiter de las cuales se puede deducir una velocidad de la luz de 2 X 108 m/seg.
Aproximadamente 50 años más tarde, James Bradley, un astrónomo inglés, hizo algunas observaciones astronómicas de naturaleza totalmente diferente, de las cuales se puede deducir un valor de 3.0 X 10 elevado a 8 m/seg. (un 3 con 8 ceros, 300000000)
En 1849, Hippolyte Louis Fizeau (1819-1896), un físico francés, fue el primero que midió la velocidad de la luz por un método no astronómico, obteniendo un valor de 3.13 X 108 m/seg.
La figuramuestra el aparato de Fizeau. Para comenzar no nos fijemos en la rueda dentada.
La luz de la fuente S se hace convergente mediante la lente L, es reflejada por el espejo M1, y forma en el espació en E una imagen de la fuente.
El espejo M, se llama “espejo semiplateado”, su capa reflectora es tan delgada que sólo la mitad de la luz que le llega es reflejada, siendo transmitida la otra mitad.
La luz de la imagen en F entra a la lente L2 y sale como un haz de rayos paralelos; después de pasar por la lente L3 es reflejada siguiendo su dirección original, pero en sentido contrario hacia el espejo M2.
En el experimento de Fizeau la distancia 1 entre M2 y F fue de 8.630 m, o sea, 5.36 millas.
Cuando la luz llega al espejo M1 otra Vez algo de ella es transmitida, entrando al ojo del observador por la lente L1.
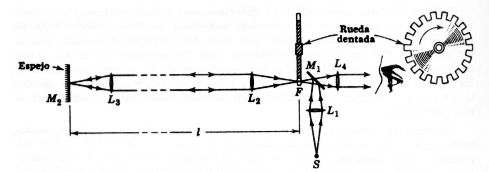
Metodo de Fizeau Para Determinar la velocidad de la luz
El observador verá una imagen de la fuente formada por la luz que ha viajado una distancia 2.L entre la rueda y el espejo M2 de ida Y regreso.
Para medir el tiempo que tarda el haz de luz en ir y regresar se necesita proveerlo, en alguna forma, de un marcador.
Esto Se hace “cortándolo” con una rueda dentada que gira rápidamente.
Supóngase que durante el tiempo de ida y vuelta 2L/c, la rueda ha girado exactamente lo necesario para que cuando una determinada «porción de luz» regresa a la rueda, el punto F está tapado por un diente.
La luz pegará contra la cara del diente que está hacia M2 y no llegará al ojo del observador.
Si la velocidad de la rueda es precisamente la adecuada, el observador no verá ninguna de las «porciones de luz” porque cada una de ellas será tapada por un diente.
El observador mide a c aumentando la velocidad angular de la rueda desde cero hasta que desaparezca la imagen de la fuente S.
Sea e la distancia angular del centro de un hueco al centro de un diente.
El tiempo que requiere la rueda para girar una distancia e; es el tiempo del viaje de ida y vuelta 2L/c. En forma de ecuación:
![]()
Esta técnica del «rayo cortado” convenientemente modificada, Se usa en la actualidad para medir las velocidades de los, neutrones y de otras partículas.
EJEMPLO NUMERICO DEL RAZONAMIENTO
La rueda usada por Fizeau tenía 720 dientes. ¿Cuál es la Velocidad angular mínima para la cual desaparecía la imagen de la fuente?
El ángulo e es de 1/1440 rev; despejando a de la ecuación anterior resulta:
![]()
 El físico francés Foucault (1819-1868) mejoró notablemente el método de Fizeau sustituyendo un espejo giratorio por la rueda dentada.
El físico francés Foucault (1819-1868) mejoró notablemente el método de Fizeau sustituyendo un espejo giratorio por la rueda dentada.
El físico norteamericano Albert A. Míchelson (1852-1931) efectuó durante un periodo de 50 años una extensa serie de medición de c, usando esta técnica.
Debemos considerar la velocidad de la luz dentro del marco más amplio de la velocidad de las radiaciones electromagnéticas en general.
Es una confirmación experimental importante de la teoría de Maxwell del electromagnetismo que la velocidad en el espacio libre de ondas en todas las partes del espectro electromagnético tiene el mismo valor c.
La tabla mas abajo muestra los resultados de algunas mediciones que se han hecho de la velocidad de la radiación electromagnética desde la época de Galileo.
Es un verdadero monumento a la perseverancia y al ingenio humano.
Nótese, en la última columna, cómo se ha mejorado la incertidumbre en las mediciones al correr de los años.
Nótese también el carácter internacional del esfuerzo y la variedad de los métodos.
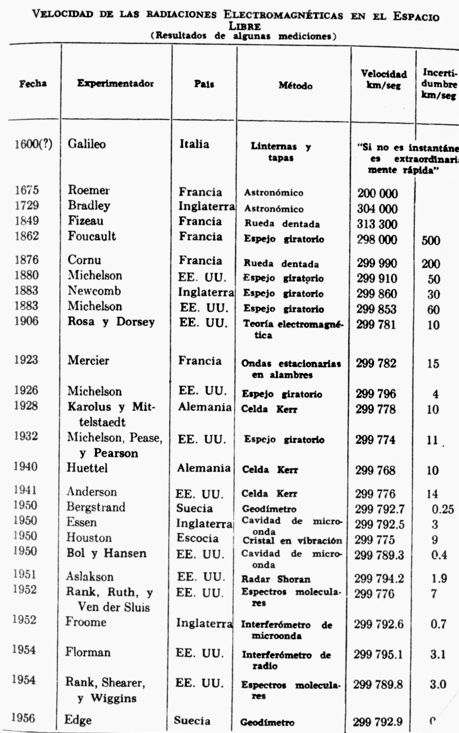
El trabajo de llegar a un solo valor “mejor” de e a partir de los muchos consignados en la tabla es difícil, porque implica un estudio cuidadoso de cada una de las mediciones efectuadas y una selección de entre ellas, fundada en las incertidumbres reconocidas por los experimentadores y el juicio del seleccionador por lo que se refiere a la presencia o ausencia probable de errores ocultos.
Al hacer el promedio final, se dará más peso a las mediciones que tengan pequeñas incertidumbres que a las que tengan grandes incertidumbres. Mediante un cuidadoso análisis de tales mediciones fue como en 1964 se llegó al “mejor” valor de c = 2.997925x 1O8 m/seg.
La incertidumbre de la medición es de menos de 0.000003 X 108 m/seg. o sea, 0,0001%
• ALGO MAS SOBRE EL TEMA...
• MÉTODO DE RÓMER
En 1670, por primera vez en la historia, el astrónomo danés Olaf Rómer pudo calcular la velocidad de la luz.
Se hallaba estudiando los eclipses de uno de los satélites de Júpiter, cuyo período había determinado tiempo atrás.
Estaba, pues, en condiciones de calcular cuándo habrían de producirse los próximos eclipses. Se dispuso a observar uno de ellos, y con sorpresa vio que a pesar de que llegaba el instante tan cuidadosamente calculado por él, el eclipse no se producía, y que el satélite demoró 1 000 segundos más en desaparecer.
Asombrado, revisó cuidadosamente sus cálculos y comprobó que eran correctos. ¿Qué había sucedido? Para comprenderlo mejor, hagamos la siguiente comparación:
imaginemos que la sirena de una fábrica .nena todos los días exactamente a las 12.
Un señor que vive a 350 m de ella la oirá a las 12 horas y 1 segundo, pues la velocidad del sonido es de 350 m/s.
Si un día este señor se va de paseo, y a las 12 se encuentra a 700 m de la fábrica, no se asombrará de oír la sirena a las 12 y 2 segundos, por que él sabe que el sonido tiene una velocidad de 350 m/s.
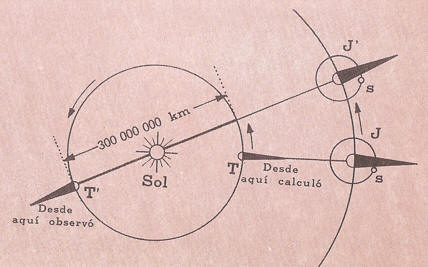
Algo muy parecido sucedió a Roemer con los eclipses del satélite de Júpiter. Rómer había hecho todos sus cálculos basándose en observaciones realizadas cuando la Tierra y Júpiter ocupaban las posiciones que en la figura señalamos T y J, respectivamente, pero cuando observó el retraso en el eclipse, las posiciones ocupadas por los planetas eran V y J'.
El dibujo muestra que entonces la luz debe recorrer una distancia suplementaria de 300 millones de km, y en ello empleó los 1.000 segundos de retraso que tanto sorprendieron a Roemer.
El astrónomo interpretó correctamente los hechos e hizo el cálculo de la velocidad de la luz.
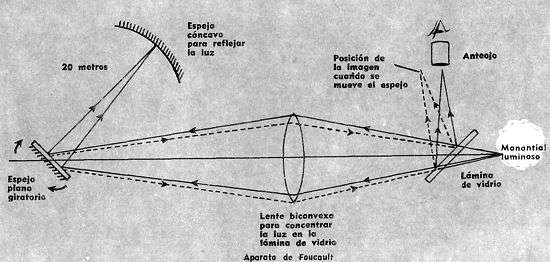
• MÉTODO DE FOUCAULT
El aparato de Foucault era mucho más sencillo que el de Fizeau y la luz recorría una distancia más pequeña.
Esto tiene la ventaja de poder medir la velocidad de la luz a través de distintos medios, llenando el espacio con dichos medios.
También se puede hacer el vacío y determinar la velocidad de la luz en el vacío.
La luz se propaga ligeramente más despacio en el aire que en el vacío; en el agua sólo tiene % de su velocidad en el aire; a través del cristal, la velocidad es menor, dependiendo del tipo de cristal.
Veamos el método de Foucault.
La luz producida en un manantial luminoso pasaba a través de una lámina de vidrio y, después, a traves de una lente convergente que la concentraba en la superficie de un espejo plano.
Otro espejo, cóncavo, se disponía de forma que la luz que reflejaba el plano llegaba a un foco y se reflejaba siguiendo el mismo camino que a la ida.
Cuando la luz llegaba de nuevo al espejo plano se reflejaba, y esta luz reflejada convergía formando una imagen de la fuente luminosa, que se observaba a través de un anteojo.
Si el espejo plano giraba, la luz que reflejaba al volver a él lo encontraba en otra posición y, por tanto, la imagen en el anteojo estaba ligeramente corrida.
La velocidad de la luz podía calcularse a partir de la velocidad de rotación, la magnitud del movimiento y la distancia entre los espejos.
Existen modificaciones del método original, que permiten obtener resultados más precisos.

- Aparato de Foucault - Medición Velocidad de la Luz
La causa de error mayor en este método era la medida del pequeño movimiento de la imagen.
Hubiera sido más conveniente hacer girar el espejo tan rápido que estuviera otra vez en la misma posición al recibir la luz reflejada.
Esto habría dado una imagen en la misma posición y sólo habrían sido necesarias en el cálculo las distancias entre los espejos y la velocidad de rotación.
Michelson resolvió este problema, sustituyendo el espejo plano por uno octogonal.
Distintas caras del octógono reflejaban la luz en su camino de ida y en el de vuelta. Así, la luz sólo era visible para el observador cuando el octógono tenía una determinada posición.
Esto ocurría si el octógono estaba quieto o si giraba a una velocidad tal que una cara sustituía exactamente a otra, mientras la luz recorría un determinado camino hasta un reflector lejano, y viceversa.
La velocidad de rotación se calculaba con bastante exactitud, y luego se usaba en el cálculo de la velocidad de la luz.
A pesar de su velocidad, la luz necesita bastante tiempo para viajar por la inmensidad del espacio.
En efecto, a la Tierra está llegando la luz de cuerpos celestes que han desaparecido hace mucho tiempo. Las distancias en el espacio son tan enormes que expresarlas en kilómetros sería ridículo.
En vez de esto, se usan años-luz.
Un año-luz es la distancia que recorre la luz, en el vacío, en un año. Si recorre 300.000 Km./seg., en un año recorrería esta distancia multiplicada por el número de segundos que tiene un año.
No se conoce nada que tenga una velocidad superior a la de la luz.
Aunque se trata de encontrar aparatos rápidos, es muy improbable que lleguen a acercarse a la velocidad de la luz.
Cuanto más rápidos, más pesados se hacen y esto les impide aumentar su velocidad.
Fuente Consultada:
Física I Resnick-Holliday Tomo I
TECNIRAMA Enciclopedia de la Ciencia y la Tecnología - El Método de Foucault -
Temas Relacionados:
Descomposición de Fuerzas en un Plano Inclinado
El Conocimiento Científico La Fisica y de la Naturaleza
El Cuanto de Energia:Fisica Cuantica
Que es un Caballo de Fuerza (HP)?
Las Leyes del Pendulo Fisico
Ventajas de la Actividad Fisica Para Mejorar la Calidad de Vida
Enlace Externo: Relatividad y Velocidad de la Luz