Acertijos de Sam Loyd Problemas Para Pensar-Con Respuestas-
Acertijos de Sam Loyd - Problemas Para Pensar -

Sam Loyd: (1841-1911) (foto) fue unos de los inventores de rompecabezas y acertijos mas grande del mundo. Todos sus trabajos fueron apareciendo en revistas y diarios durante mas de 50 años en los EE.UU., por lo que goza una gran popularidad.
Fue el inventor del acertijo mecánico del 15, esa cajita cuadrada con mas cuadraditos numerados (del 1 al 15) adentros móviles que deben ordenarse de menor a mayor. Inclusive algunos de sus acertijos se han utilizado para campañas publicitarias de importantes candidatos a la presidencia de los EE.UU.
Sobre el ajedrez escribió: "como hijo de ricos, pero respetables padres y como el más joven de ocho hermanos, mis primeros recuerdos están vinculados inseparablemente al tablero de ajedrez.
Desde el principio de mi vida tenía un afecto especial por los rompecabezas y trucos y trabajé ya con problemas de ajedrez, antes de cumplir 12 años me encantaba este arte tanto, para que esta dedicación intensa haya resistido todas las vicisitudes de la vida durante todos los años ".
Se lo considera como unos de los mejores compositores de problemas, dotado de un talento especial para la matemática le ha permitido plantear innumerables de problemas creativos y curiosos que desafían a los grandes matematicos del siglo y lo sorprendente es que la mayoría de sus creaciones las elaboró antes de cumplir sus 20 años de edad.

• EJERCICIO DE SAM LOYD 1

1)¿Que distancia recorre la pelota?
Si se arroja una pelota de goma desde la Torre de Pisa, de 179 pies de altura, y en cada rebote la pelota se eleva un décimo de la altura inmediata anterior. Puede calcular, que distancia recorre antes de quedarse quieta?

• EJERCICIO DE SAM LOYD 2

2) ¿Cuál es el ancho del rio?
Dos ferrys simultamente en marcha en márgenes Opuestas del río Hudson. Uno. de ellos va de New York a Jersey City, y el otro de Jersey City a New York. Uno es más rápido que el otro, de modo que se encuentran a 720 yardas de la costa más próxima.
Tras llegar a destino, ambas embarcaciones perrnanecen diez minutos en el muelle Para cambiar el pasaje, y luego emprenden el viaje de regreso. Vuelven a encontrarse esta vez a 400 yardas de la otra costa. ¿Cuál es la anchura exacta del río?
El problema muestra que la persona normal, que sigue las reglas rutinarias de la matemática, quedará perpleja ante un problema simple que requiere tan sólo un conocimiento superficial de la aritmética elemental.
Un niño podría resolverlo y, no obstante, me atrevo a arriesgar la opinión de que el 99% de lo hombre de negocios no llegarán a resolverlo en una semana. De eso sirve aprender matemáticas por medio de reglas en vez de hacerlo por medio del sentido común, que siempre nos dá la razón!. Sam Loyd

• EJERCICIO DE SAM LOYD 3

3) ¿Cuánto pesa el ladrillo?
Observa la figura y determina cuanto pesa el ladrillo de la izquierda, si para equilibrarlo hace falta otro de 3/4 más 3/4 de 1(una) libra?.

• EJERCICIO DE SAM LOYD 4

4) Rescate: El método de Bink de salvataje contra incendios es simplemente una soga que pasa por una polea y tiene en cada extremo una gran canasta. Cuando una canasta baja, la otra sube.
Colocando un objeto en una de las canastas para que actúe como contrapeso, un objeto más pesado puede ser bajado en la otra canasta.
El Inventor dice que su aparato debe ser colgado afuera de todos los dormitorios del mundo.
El sistema fue adoptado en un hotel, pero los huéspedes delincuentes lo utilizaron para escapar durante la noche sin pagar, por lo que el mecanismo no siguió contando con la aprobación de los hoteleros.
El dibujo muestra un ascensor Blnks situado ante la ventana de un moderno hotel veraniego.
Nada que pese más de treinta libras puede ser bajado con seguridad en una canasta mientras la otra está vacia, y treinta libras es el limite de seguridad de la diferencia que puede existir entre ambas canastas cuando las dos llevan un peso.
Una noche se desató un incendio en el hotel, y todos los huéspedes lograron escapar excepto el vigilante nocturno y su familia.
No pudieron ser despertados hasta que todas las vías de escape, excepto el ascensor Binks, estuvieron cerradas. El vigilante pesaba 90 libras, sil esposa 210 libras, el perro 60 libras y el bebé 30 libras.
Cada canasta tiene capacidad para los cuatro, pero no pueden usarse pesos en las canastas sólo el hombre, su esposa, el perro y el bebé.
Si suponemos que nl el perro ni el bebé son capaces de entrar o salir de la canasta sin la ayuda del hombre o de su esposa, ¿cuál es la manera más eficiente

• EJERCICIO DE SAM LOYD 5

5) La señora Hubbard ha ideado un inteligente sistema para controlar sus frascos de dulce de mora. Ha distribuido los frascos en la alacena (ver el dibujo) de manera de tener veinte cuartos de dulce en cada estante.
Los frascos son de tres tamaños diferentes. Puede decir Ud. que cantidad contiene cada uno de los tamaños?

• EJERCICIO DE SAM LOYD 6

¿Cuál es la longitud del cable?
La investigación de la Luna ejerce una fascinación irresistible. Cuando el público, a principios del siglo pasado, sufrió el famoso "engaño de la Luna", quedó demostrado que la gente estaba dispuesta a creer casi cualquier cosa acerca de la Luna.
El engaño se basaba en los supuestos poderes de un telescopio maravilloso, y el publico aceptó los informes con tanta credulidad que los responsables del engaño pudieron suministrar vividas descripciones de los habitantes de la Luna y de sus bellos paisajes.
A pesar de la extravagancia de esas descripciones, fueron aceptadas como hechos por muchos miles de personas.
Muchos escritores han producido especulaciones acerca de la situación de la Luna. Ariosto, en su Orlando Furioso, mandó a Astolfo a la Luna en un viaje azaroso y accidentado, y su relato de lo que vio en el Valle de las Cosas Perdidas engañó a muchas personas.
El viaje a la Luna de Cyrano de Bcrgerac es uno de los más entretenidos aportes de la literatura, y el relato más reciente de Julio Verne acerca de mi viaje a la Luna es tal vez el más estremecedor cuento lunar.
Un meticuloso relato de Edgar Allan Poe incidió tanto sobre la mente de un erudito profesor llamado Spearwood que este último preparó una expedición, intentando hacer el viaje en globo.
Mi ilustración está inspirada en una descripción de la época del ascenso. El globo está unido a una esfera de cable de acero, y este cable tiene un espesor de un centesimo de pulgada.
Suponiendo que la esfera de cable tuviera originariamente un diámetro de dos pies (24 pulgadas), y que estuviera tan apretadamente enrollada que no permitiera el menor espacio hueco, ¿podría alguno de nuestros aficionados calcular la longitud total del cable?

• EJERCICIO DE SAM LOYD 7

¿Cuánto oro tenía el avaro?
Un avaro, antes de morirse de hambre, acumuló una cantidad de monedas de oro de cinco, diez y veinte dólares, las guardaba en cinco bolsas que eran exactamente iguales en cuanto a que todas contenían la misma cantidad de monedas de cinco dólares, el mismo número de monedas de diez dólares y el mismo número de monedas de veinte dólares.
El avaro contaba su tesoro poniendo todas las monedas sobre la mesa y dividiéndolas luego en cuatro pilas que también contenían la misma cantidad de cada tipo de monedas.
Su último paso era tomar dos cualesquiera de estas pilas, reunir las monedas y distribuirlas luego en tres pilas que eran exactamente iguales en el sentido ya explicado. Resulta ahora fácil adivinar cuál es la menor cantidad de dinero que debe haber poseído este pobre anciano.

• EJERCICIO DE SAM LOYD 8

¿Qué circunferencia recorre?
Recientemente, mientras disfrutaba de una caminata por el campo con un amigo, nos encontramos con su hijo, quien conducía un sulky.
El vehículo describió un giro cerrado que amenazaba la estabilidad del sulky y también la de los nervios del padre del conductor. Cuando regresamos a casa, padre e hijo se enzarzaron en una viva discusión con respecto a las posibilidades de giro del vehículo.
En la ilustración vemos al hijo demostrando su habilidad para conducir el sulky en círculos y sin volcarlo.
Las ruedas exteriores están separadas de las interiores por dos ejes de cinco pies de largo, y las exteriores dan dos vueltas por cada vuelta que dan las ruedas interiores.
El problema consiste en determinar la circunferencia del círculo que describen las ruedas exteriores.

• EJERCICIO DE SAM LOYD 9

¿Qué barril quedó?
Cada uno de los barriles en la ilustración adjunta contiene aceite o vinagre. El galón de aceite cuesta el doble que el de vinagre. Un cliente compra $ 14 de cada uno, dejando un solo barril ¿Qué barril queda?

• EJERCICIO DE SAM LOYD 10

¿Cuánto pesa un cubo?
El inspector Jones, cuyo trabajo consiste en controlar la precisión de las balanzas que se utilizan en la ciudad, acaba de descubrir una mal calibrada.
Un brazo es más largo que el otro, pero el peso de los platillos da impresión de equilibrio. (No hay que juzgar por las apariencias en la ilustración, pues me he tomado una licencia como inventor de acertijos, y dibujé la balanza de tal modo de no revelar la clave).
Cuando el inspector puso tres pesas piramidales en el brazo largo, se equilibraron con ocho pesas cúbicas que puso en el brazo más corto. ¡Pero cuando puso un cubo en el brazo largo, se equilibró con seis pirámides puestas en el brazo corto! Suponiendo que el verdadero peso de una pirámide es una onza, ¿puede usted determinar el verdadero peso de un cubo?

• EJERCICIO DE SAM LOYD 11
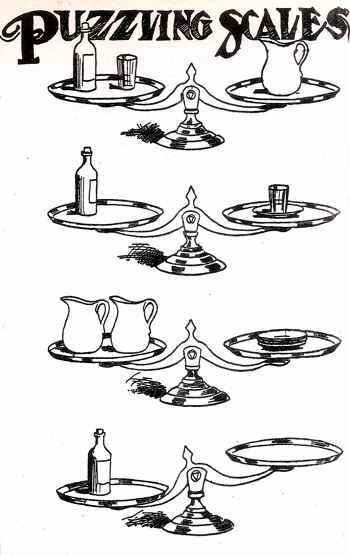
¿Cuántos vasos serán necesarios para equilibrar la botella?

• EJERCICIO DE SAM LOYD 12

¿Qué tamaño tiene la boca del caldero?
El calderero acaba de terminar un caldero de base plana, de doce pulgadas de profundidad y que contiene exactamente 5.775 pulgadas cúbicas de agua.
¿Cuántos de nuestros matemáticos pueden decirnos (con aproximación a pulgadas) el diámetro de la boca del caldero, suponiendo que es el doble del diámetro de la base?.

• EJERCICIO DE SAM LOYD 13


• EJERCICIO DE SAM LOYD 14

Acertijo del Tonto
¿Cómo pueden disponerse estos tres niños para que los dígitos marcados en sus ropas formen un número de tres cifras que sea divisible por siete?
(usa tu pensamiento lateral)

• EJERCICIO DE SAM LOYD 15

Una curiosa cadena de reloj, diseñada según la vieja costumbre de llevar una ristra de monedas unida a un reloj. Esta cadena en particular consistía en cuatro monedas y la efigie de un águila.
Las monedas, tal como se ve en la ilustración, tenían respectivamente cinco, cuatro, tres y dos perforaciones, de modo que los eslabones que las unían podían haber sido situados de maneras diferentes, suministrando una variedad de diseños.
Esta particularidad de poder producir una serie de cadenas de reloj, con una ristra de cuatro monedas uniendo el reloj con el águila, dio lugar a una discusión acerca del número de disposiciones posibles diferentes que pueden lograse con las cinco piezas.
¿Qué opina usted?.

• EJERCICIO DE SAM LOYD 16

Se cuenta que un lechero honesto y simplón, que alardeaba mucho de su corrección y del hecho de no haber desilusionado jamás a un cliente, descubrió con desagrado una mañana que su provisión de leche era inadecuada para la demanda de sus clientes.
En efecto, su stock era demasiado escaso para abastecer su ruta habitual, y no tenía ninguna posibilidad de conseguir más leche.
Advirtiendo el pésimo efecto que esto podría tener sobre su negocio, por no hablar de la decepción y la incomodidad que produciría a sus clientes, se rompía la cabeza pensando qué podía hacer.
Tras darle muchas vueltas a la cuestión, decidió que era demasiado consciente y justo como para atender a algunos y pasar por alto a otros. Tendría que dividir lo que tenía entre todos, así que diluiría la leche con la cantidad de agua suficiente como para abastecer todas las demandas.
Cuando halló, tras una diligente búsqueda, un poco de agua extremadamente pura que podía emplear tranquilamente para su propósito, puso en uno de los tarros la cantidad de galones de agua que le permitiría atender a todos sus clientes.
Sin embargo, como acostumbraba vender leche de dos calidades, una por ocho centavos el cuarto, y la otra por diez, se dispuso a producir dos mezclas de la siguiente ingeniosa manera:
Del tarro número 1, que sólo contenía agua, vertió una cantidad suficiente como para duplicar el contenido del tarro número 2, que sólo contenía leche.
Después, vertió del número 2 al número 1 una cantidad de la mezcla igual a la cantidad de agua que había dejado en el número 1.
Después, para asegurarse las proporciones deseadas, procedió a verter del número 1 la cantidad suficiente para duplicar el contenido del número 2.
Esto dejó igual cantidad de galones en cada tarro, como puede demostrarse, aunque en el tarro número 2 había dos galones más de agua que de leche.
Ahora bien, el proceso no es tan complicado como parece, pues sólo hacen falta tres cambios para igualar los contenidos de ambos tarros. ¿Puede determinar exactamente cuánta agua y cuánta leche contenía finalmente cada tarro?

• EJERCICIO DE SAM LOYD 17

El enigma de los gatos y los gatitos:
Viendo que cuatro gatos y tres gatitos pesan 37 libras, mientras que tres gatos y cuatro gatitos pesan 33 libras, se nos plantea cual es el peso de los gatos y los gatitos.

• RESPUESTAS
1)- La pelota recorrería una distancia de 218,77777 pies.
2) Cuando los ferry se cruzan en el punto X están a 720 yardas de una de las costas. La distancia que han recorrido entre ambos es igual a la anchura del río.
Cuando llegan a la costa opuesta, la distancia sumada es igual al doble de la anchura del río.
En el viaje de regreso se encuentran en el punto Z después de haber recorrido entre ambos una distancia igual a tres veces la anchura del río, de modo que cada embarcación ha recorrido tres veces la distancia que cada una de ellas había andado cuando se encontraron por primera vez.
En el primer encuentro, uno de los botes había recorrido 720 yardas, de modo al llegar a Z debe haber recorrido (res veces esa distancia, es decir 2.160 yardas.
Como muéstra el diagrama, esta distancia es 400 yardas mayor que la anchura del río, de modo que todo el trabajo matemático que debemos hacer es deducir 400 de 2.160 para obtener la anchura del río.
El resultado es 1.760 yardas, exactamente una milla.
El tiempo que pierde cada uno de los barcos en el amarradero no afecta el problema.
3) La pesa de 3/4 sw libra es claramente igual a 1/4 de ladrillo, por lo tanto , cada ladrillo debe pesar 12/4, osea 3 libras.
4) El guardián, su esposa, el bebé y el perro escapan de la siguiente manera:
1. Baja el bebé.
2. Baja el perro, sube el bebé.
3. Baja el hombre, sube el perro.
4. Baja el bebé.
5. Baja el perro, sube el bebé.
6. Baja el bebé.
7. Baja la esposa, suben todos los otros.
8. Baja el bebé.
9. Baja el perro, sube el bebé.
10. Baja el bebé.
11. Baja el hombre, sube el perro.
12. Baja el perro, sube el bebé.
13. Baja el bebé.
(Esta es una versión simplificada del problema propuesto por Lewis Carroll, que puede encontrarse en The l-ewis Carroll Picture Book, editado por Stuart Dodgson Co-llingwood, 1899. — M.G.)
5) Sabiendo que cada anaquel contiene exactamente veinte cuartos, empecemos por eliminar seis frascos pequeños de cada uno de los dos anaqueles inferiores.
Nos quedan dos frascos grandes en el estante del medio y cuatro medianos en el anaquel inferior, lo que demuestra que un frasco grande contiene tanto dulce como dos medianos.
Restituyamos los frascos cancelados, y cancelemos entonces los dos grandes del estante intermedio y su equivalente en el anaquel superior: un frasco grande y dos medianos.
Esto nos deja con un frasco mediano y tres pequeños en el anaquel superior y seis frasquitos en el anaquel del medio, demostrando que un frasco mediano contiene tanto dulce como tres de los más pequeños.
Ahora restituyamos todos los frascos grandes, reemplazándolos por dos frascos medianos y luego reemplacemos los frascos medianos con tres pequeños.
Esto nos da un total de 54 frasquitos. Si 54 frasquitos contienen 60 cuartos, uno contendrá 1 cuarto y 1/9, un frasco mediano contendrá 3 cuartos y 1/3 y un frasco grande, 6 cuartos y 2/3.
6) Para resolver este problema sin hacer uso de pi, es necesario recordar el gran descubrimiento de Arquímedes de que el volumen de una esfera es igual a dos tercios del volumen de una caja cilindrica en la que la esfera encaja exactamente.
La esfera de cable tiene un diámetro de 24 pulgadas, de modo que su volumen es igual al de un cilindro de 16 pulgadas de altura y con un diámetro de base de 24 pulgadas.
Ahora bien, el cable es simplemente un cilindro extendido.
¿Cuántas partes de cable, cada una de 16 pulgadas de altura y de un centesimo de pulgada de diámetro, son iguales en volumen al cilindro de 16 pulgadas de altura y de 24 pulgadas de diámetro de base? Las superficies de los círculos guardan entre sí la misma proporción que los cuadrados de sus diámetros.
El cuadrado de 1/100 es 1/10.000, y el cuadrado de 24 es 576, por lo que concluimos que el volumen del cilindro es igual a 5.760.000 de los cables de 16 pulgadas de longitud. La longitud total del cable, por lo tanto, es 5.760.000 por 16, o 92.160.000 pulgadas.
7) Como el avaro podía dividir cada tipo de moneda parejamente en cuatro, cinco y seis partes, debe haber tenido por lo menos sesenta monedas de cada clase, haciendo un total de 2.100 pesos.
8) Para que las ruedas exteriores vayan al doble de velocidad que las ruedas interiores, el circulo exterior debe tener el doble de la circunferencia del circulo interior.
Por lo tanto los cinco pies que separan a las ruedas interiores de las exteriores deben representar la mitad del radio del círculo exterior , dando a este circulo un diametro de 20 pies y una circunferencia que es Pi=3.14 veces 20, es decir 62,832 pies.
9) El cliente compró los barriles de aceite de 13 y 15 galones a 50 ctvos. por galón y los barriles de vinagre de 31,18 y 8 galones a 25 ctv. por galón. Esto deja al barril de 19 galones que puede contener tanto aceite como vinagre.
10) Una buena regla para recordar en los casos de balanzas falsas como las que aquí se describen es: pesar un artículo en un brazo de la balanza y después en el otro, multiplicar ambos resultados, y la raíz cuadrada del resultado será el peso verdadero del artículo.
Sabiendo que una pirámide pesa una onza, el primer pesaje del inspector demostró que un cubo pesa 3/8 de onza. Su segundo pesaje, con el cubo en el otro brazo, demostró que un cubo pesaba seis onzas.
Seis por 3/8 es 18/8 o 9/4, cuya raíz cuadrada es 3/2 o 1 onza y media. Por lo tanto, un cubo pesa una onza y media y, en una balanza fiel, ocho cubos se equilibrarían con doce pirámides.
11) Dos jarras se equilibran con tres platos, de modo que sabemos que un plato es igual a 2/3 de una jarra.
Ahora agreguemos un vaso en cada platillo de la balanza en la segunda ilustración, para hacer que el brazo izquierdo sea igual al brazo izquierdo de la primera ilustración.
Esto prueba que una jarra es igual a un plato y dos vasos; y como un plato es igual a 2/3 de una jarra, los dos vasos deben compensar el tercio faltante. Cada vaso, por lo tanto, representa 1/6 de la jarra.
En la primera ilustración vemos que un vaso (1/6 de la jarra) y una botella se equilibran con una jarra, lo que nos dice que una botella debe representar 5/6 de la jarra. Por lo tanto, para equilibrar la botella en la última ilustración necesitaremos cinco vasos.
12) El caldero, al igual que un balde o la pantalla de una lampara, tiene la forma de un cono truncado, que es simplemente un cono con la parte superior cortada paralelamente a la base. Su volumen puede calcularse sustrayendo el cono cortado del cono más grande, o de manera más simple mediante la fórmula:
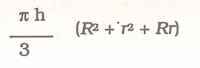
En esta fórmula, h representa la altura del cono truncado, y R mayúscula y minúscula el radio del tope y de la base.
Con respecto al caldero, sabemos que su altura es 12 pulgadas, y que un radio es el doble del otro. Si R es el radio de la base y 2R el radio del tope, el volumen será pi (3.14) veces 28R².
Como el volumen es de 5.775 pulgadas cúbicas, es fácil calcular que el diámetro de la boca es un poco más de 32 pulgadas.
13) El joyero robo una gema de cada extremo de la fila horizontal, luego simplemente llevó el diamante inferior hacia arriba.
Puede ayudarte con un dibujo para ver la solcución.
14) El chico non el número 6 se paró de cabeza abajo,de modo que tres pudieran formar el número 931.
15) Los matemáticos y los aficionados que se deleitan con los misterios de las permutaciones han calculado que se pueden hacer alrededor de 92.160 cadenas diferentes con las cuatro monedas y el águila colgante, sin que dos de ellas sean iguales.
Es evidente que la moneda grande puede ser suspendida de cualquiera de los 5 agujeros, y con cualquiera de las 2 caras mirando al frente, lo que admitiría 10 variantes posibles.
Como el centavo puede ser colocado en 8 posiciones, estas dos monedas solas representarían 80 combinaciones que, multiplicadas por las 6 posiciones del penique, y por las 4 variantes de la otra y las 2 posiciones del águila, demuestran que en el orden de tamaños en el que ahora están enhebradas podría haber 3.840 cambios.
Como existen 24 variantes a partir de la simple variación en el orden de las monedas, 3.840 veces 24 da 92.160 como respuesta correcta a este acertijo.
16) El honesto lechero empezó con 5 galones de leche en el tarro N º 2 y 11 de agua en el tarro N º 1. Las operaciones descritas darán como resultado 6 galones de agua y 2 de leche en el primer tarro, y 5 galones de agua y 3 de leche en el segundo tarro.
17) Podemos comprobar que la balanza superior contiene un gato más y un gatito menos que la balanza inferior y la diferencia es de 4 libras.
Uno de los gatitos de la balanza inferior, se convierte de repente en un gato y gana 4 libras de peso, por lo tanto, la diferencia de peso entre un gato y un gatito es de 4 libras.
Si cambiamos todos los gatos de la balanza superior por gatitos, tendríamos entonces que 7 gatitos y 16 libras se equilibran con 37 libras.
Ahora, quitamos 16 libras de ambos extremos de la balanza y tenemos que 7 gatitos se equilibran con 21 libras, lo que demuestra que cada gatito pesa 3 libras y por lo tanto, cada gato pesa 7 libras.
![]()
AMPLIACIÓN DEL TEMA...
LA ERA DE LAS ADIVINANZAS, LOS ACERTIJOS Y LOS ENIGMAS
Desde la época de los griegos, los matemáticos han buscado darle color a sus libros de texto parafraseando sus demostraciones y teoremas en forma de acertijos numéricos.
Durante la segunda mitad del siglo XIX esta aproximación juguetona al tema encontró su lugar en la prensa popular, y los acertijos numéricos iban al lado de los crucigramas y anagramas.
Al cabo del tiempo había una audiencia creciente para los acertijos matemáticos, pues los aficionados consideraban cualquier cosa, desde los acertijos más triviales hasta los más complejos problemas matemáticos, entre ellos el último teorema de Fermat.
Quizás el más prolífico creador de acertijos fue Henry Dudeney, que escribió docenas para periódicos y revistas, dentro de las que se cuentan Strand, Cassell's, Queen, Tit-Bits, Weekly Dispatch y Blighty.
Otro de los grandes creadores de acertijos de la época victoriana fue el reverendo Charles Dodgson, profesor de matemáticas en Christ Church, Oxford, y mejor conocido como el autor Lewis Carroll.
Dodgson dedicó varios años a hacer un gran compendio de acertijos con el título de Curiosa Mathematica, y aunque nunca completó la serie, sí escribió varios volúmenes, entre ellos Problemas para la almohada.
El más grande de todos los creadores de acertijos fue el prodigio estadounidense Sam Loyd (1841-1911), que de adolescente comenzó a obtener considerables ganancias creando acertijos nuevos y reinventando algunos viejos.
Él mismo recuerda en Sam Loyd y sus acertijos: una reseña autobiográfica que algunos de sus primeros acertijos los creó para el empresario circense y embaucador P. T. Barnum:
Hace muchos años, cuando el circo ele Barnum era de verdad "el espectáculo más grande del mundo", el famoso empresario hizo que le preparara una serie de acertijos para propósitos publicitarios.
Llegaron a ser conocidos ampliamente como las "preguntas de la esfinge" por cuenta de los grandes premios que se ofrecían a quienes pudieran resolverlos.
Extrañamente, esta autobiografía fue escrita en 1928, diecisiete años después de la muerte de Loyd.
Loyd pasó su astucia a su hijo, también llamado Sam, quien era el verdadero autor del libro y sabía muy bien que cualquiera que lo comprara asumiría equivocadamente que había sido escrito por el más famoso Sam Loyd padre.
La creación más famosa de Loyd fue el equivalente Victoriano del cubo de Rubik, el acertijo 14-15, que todavía se encuentra en las jugueterías.
Quince cuadrados pequeños numerados del 1 al 15 se encuentran en una marco de 4x4. y el objetivo es deslizar los cuadrados hasta que queden en el orden correcto. (jugar a este juego mas abajo)
El acertijo 14-15 de Loyd se vendía con los cuadrados colocados como se muestra en la figura 14 y Loyd ofrecía una recompensa considerable a quien pudiera com pletar el acertijo colocando el 14 y el 15 en sus posiciones correctas mediante una serie de deslizamientos.
El hijo de Loyd escribió sobre el escándalo que generó este acertijo con creto pero esencialmente matemático:
Un premio de mil dólares, que se ofreció para la primera solución correcta del problema, jamás ha sido reclamado, aunque hay miles de personas que sostienen haber ejecutado la proeza requerida.
La gente se encaprichó con el acertijo y se cuentan relatos risibles acerca de tenderos que se negaron a abrir sus tiendas, y acerca de un clérigo distinguido que estuvo parado toda una noche de invierno bajo un poste de luz tratando de recordar cómo había ejecutado la proeza.
El rasgo misterioso del acertijo es que nadie parece acordarse de la secuencia de movimientos mediante los cuales, están seguros, resolvieron el acertijo. Se habla de pilotos que destrozaron sus naves y de maquinistas que no detenían sus trenes en las estaciones.
Un famoso editor de Baltimore cuenta cómo salió a almorzar y fue descubierto por su frenético personal, pasada la medianoche, empujando pedacitos de pastel en el plato.
Loyd estaba seguro ele que nunca tendría que pagar los mil dólares porque sabía que es imposible intercambiar solamente dos piezas sin destruir el orden en algún otro lugar del acertijo.
De la misma manera en que un matemático puede demostrar que una ecuación no tiene soluciones, Loyd podía demostrar que su acertijo 14-15 tampoco la tenía.

Ejercicios de Lógica Matemática con Series Numéricas y de Imágenes
Puede Acceder a Mas Problemas de Sam Loyd
Fuente Consultada: El Último Teorema de Fermat Simón Singh
Algunos Link de Interés Relacionados Con Este Tema:






