Demostración pitagórica del número irracional de la raíz cuadrada de 2
Demostración pitagórica del número irracional de la raíz cuadrada de 2
El argumento pitagórico original sobre la irracionalidad de la raíz cuadrada de 2 dependía de una clase de argumento llamado reducción al absurdo: suponemos de entrada la verdad de una afirmación, seguimos sus cconsecuencias y desembocamos en una contradicción, lo que nos permite determinar su falsedad.

Poco se sabe acerca de la vida de Pitágoras antes de su llegada a Crotona, en 530 a.C. Nacido en Sanaos, una isla del mar Egeo, habría viajado por Egipto y Mesopotamia, iniciándose en las ciencias y religiones de esos lugares. Seguramente sólo se trataba de leyendas destinadas a darle el perfil del sabio ideal. Sin embargo, quedó establecido que en 530 a.C.
Tomemos un ejemplo moderno y consideremos el aforismo del gran físico del siglo veinte, Niels Bohr: “Lo contrario de cualquier gran idea es otra gran idea.”
Si la afirmación fuera cierta sus consecuencias podrían ser como mínimo algo peligrosas. Consideremos por ejemplo lo contrario de la Regla de Oro evangélica o de las prescripciones contra la mentira, o del precepto “no matarás”.
Consideremos pues si el mismo aforismo de Bohr es en si una gran idea, Si así es, la afirmación contraria, “lo contrario de cualquier gran idea no es una gran idea” también debe ser cierta.
Hemos llegado entonces a una reducción al absurdo. Si la afirmación contraria es falsa podemos dejar de lado el aforismo porque ha confesado claramente que no es una gran idea.
Presentamos aquí una versión moderna de la demostración de la irracionalidad de la raíz cuadrada de 2 utilizando la reducción al absurdo y un álgebra sencilla en lugar de la demostración exclusivamente geométrica descubierta por los pitagóricos. El estilo del argumento, el modo de pensar, son por lo menos tan iinteresantes como la conclusión:
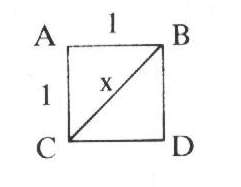
Consideremos un cuadrado cuyos lados tienen una longitud unidad o un centímetro, un metro, un año un lo que sea).
La línea diagonal BC divide al cuadrado en dos triángulos, cada uno de los cuales contiene un aángulo recto. En estos triángulos rectángulos es válido el teorema de Pitágoras:
1² + 1²= X2. Pero 1²+1²=2 , por lo tanto x2 = 2 y escribiremos x=sqr(2) , raíz cuadrada de dos.
Supongamos que sqr(2) (raiz cuadrada de 2) sea un número racional: sqr(2)=p/q. donde p y q son números enteros.
Pueden ser tan grandes como queramos y representar los números enteros que queramos. Podemos exigir desde luego que no tengan factores comunes. Si quisiéramos afirmar por ejemplo que sqr(2)= 14/10, eliminaríamos el factor común 2 y escribiríamos p=7 y q=5, no p=14 y q=10.
Hay que eliminar cualquier factor común de numerador y denominador antes de empezar.
Tenemos para escoger un número infinito de pes y de qus. Si elevamos al cuadrado los dos términos de la ecuación sqr(2)=p/q, obtenemos 2=p2/q2, y luego multiplicando ambos términos dc la ecuación por q2 llegamos a:
![]()
Por lo tanto p2 es algún número multiplicado por 2. Es decir que p2 es un número par. Pero el cuadrado de cualquier numero impar es también impar (1²=1 , 3²2=9 , 5²=25, etc.).
Por lo tanto tamhién p ha de ser par, y podemos escribir 2s, siendo s algún entero. Si sustituimos este valor de p en la ecuación anterior obtenemos:
![]()
Dividiendo ambos miembros de esta última igualdad por 2, obtenemos:
![]()
Por lo tanto q2 es también un número par y se deduce por el mismo argumento utilizado con p que q también es un número par. P
ero si p y q son ambos números pares, ambos divisibles por 2, no se redujeron a su mínimo común denominador, lo cual contradice uno de nuestros supuestos. Reducción al absurdo.
El argumento no puede decirnos que esté prohibido reducir los factores comunes, que 14/10 esté permitido y en cambio 7/5 no lo esté. Luego el supuesto inicial ha de ser erróneo; p y q no pueden ser números enteros, y sqr(2) es irracional. De hecho sqr(2)=1,4142135...
¡Qué conclusión más asombrosa e inesperada! ¡Qué demostración más elegante! Sin embargo los pitagóricos se sintieron obligados a ocultar este gran descubrimiento.
La escuela pitagórica encerraba su caducidad en si misma. A fuerza de estudiar los números. Filolao y otros discípulos del maestro comprobaron, con gran sorpresa por su parte, que algunos de entre ellos eran irracionales. ¿Cómo construir un universo sobre unos números que no podían identificarse con ningún otro?.
Dentro del fruto anidaba el gusano de la contradicción y el arsenal matemático de los pitagóricos no era suficientemente rico para soslayar esta dificultad mayor. He aquí el motivo de que Platón (497-347) se viera obligado a fundamentar su física sobre la geometría y especialmente sobre la teoría de los sólidos, de moda en su época.
Fuente Consultada: Cosmos de Carl Sagan.
Temas Relacionados:
Las Ciencias en Grecia Antigua:Cientificos Griegos
Cientificos Griegos-La Ciencia en Grecia Antigua - Cronologia
Grandes Matematicos Griegos y sus Aportes
Historia de Ciencia Tecnica Tecnologia y Sus Avances
Biografía de Isocrates: Educador en Antigua Grecia y Obra Literaria
Sólidos Platónicos Poliedros Regulares:Demostración de Pitágoras
Demostración pitagórica del número irracional de la raíz cuadrada
Enlace Externo:• El ABC de las Matemáticas | Aula Abierta






