Sólidos Platónicos,Poliedros Regulares:Demostración de Pitágoras
POLIEDROS O SÓLIDOS PLATÓNICOS - DEMOSTRACIÓN
Para los geómetras griegos, el estudio de los poliedros fue muy Importante y conocieron la existencia de los cinco únicos sólidos regulares, a los que Platón recurrió Incluso para explicar la creación del universo.
Sin embargo, no consta que conocieran un importante resultado relativo al número de vértices, aristas y caras de un poliedro convexo, observado ya por Descartes en 1640 y del que el matemático suizo Leonhard Euler dio una famosa demostración en 1752.
Euler demostró que, si se suma el número de caras y el número de vértices de un poliedro convexo y, del valor obtenido, se resta entonces el número de aristas, el resultado es siempre igual a 2.
De este resultado, válido para todo poliedro convexo, se deduce fácilmente la existencia de únicamente cinco poliedros regulares.
Definición de Poliedro:
Los cuerpos geométricos existen en el espacio y son, por tanto, objetos tridimensionales limitados por una o varias superficies.
Si todas las superficies que lo limitan son planas y de contorno poligonal, el cuerpo es un poliedro.
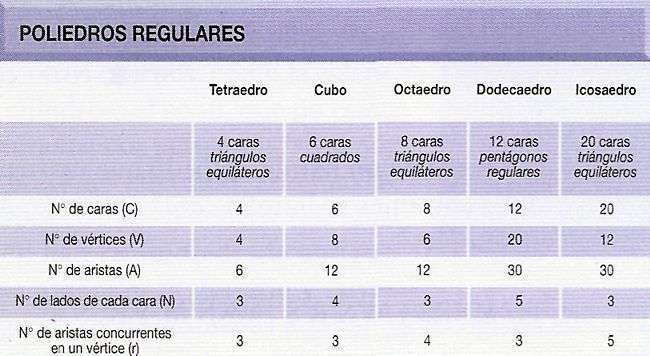
Los antiguos griegos conocían la existencia de cinco poliedros regulares, cuyo descubrimiento atribuyeron algunos al propio Pitágoras.
Teeteto fue probablemente el autor de la primera construcción teórica rigurosa de dichos poliedros como cuerpos inscritos en una esfera, construcción con la que culminaban los Elementos de Euclides, donde aparece asimismo, como colofón de la obra, la demostración de que sólo pueden existir cinco de ellos.
Pero hay otros cuerpos, como la esfera, el cilindro o el cono, que no están limitados por polígonos, sino por superficies curvadas; son los llamados cuerpos redondos, que también han recibido desde antiguo una atención preferente y cuyas superficies y volúmenes estaban ya recogidos en la obra de Euclides.
Los siguientes poliedros regulares son los llamados "poliedros platónicos".


Leonhard Euler (1707-1783)
fue un matemático suizo, verdadero virtuoso de las matemáticas, a todas cuyas ramas contribuyó en alguna medida, además de reatar aportaciones a otras ciencias, como la física y la astronomía. Autor de los primeros tratados sistemáticos del cálculo infinitesimal, convirtió la idea de función en concepto básico del análisis matemático.
Se ocupó de las funciones trascendentes y de la vinculación de ios logaritmos con los números imaginarios y las funciones circulares. Fue profesor en las Academias de Berlín y de San Petersburgo.
------------- 00000 ------------
DEMOSTRACIÓN MATEMÁTICA
Un polígono (que significa en griego “de muchos ángulos”) regular es una figura bidimensional con un cierto número n de lados iguales.
Sin = 3, el polígono es un triángulo equilátero; si n = 4 es un cuadrado; si n = 5 es un pentágono, etc.
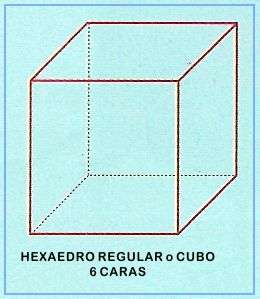
Un poliedro (que significa en griego “de muchas caras”) es una figura tridimensional cuyas caras son todas polígonos: un cubo, por ejemplo, cuyas caras son 6 cuadrados.
Un poliedro simple, o sólido regular, es un poliedro sin agujeros.
Un hecho fundamental en la obra de los pitagóricos y de Johannes Kepler es que sólo hay y puede haber 5 sólidos regulares.
La demostración más fácil deriva de una relación descubierta mucho después por Descartes y por
Leonhard Euler que relaciona el número de caras, C, el número de aristas, A y el número de vértices, V, de un sólido regular:
V-A+C=2 (2)
En un cubo, por ejemplo, hay 6 caras (C=6), y 8 vértices (V=8), 8-A+6=2 , 14-A=2, y A=12 ; la ecuación (2) predice que el cubo tiene 12 aristas, y así es.
Puede consultarse una demostración geométrica sencilla de la ecuación (2) en la obra de Courant y Robbins citada en la bibliografía.
A partir de la ecuación (2) podemos demostrar que sólo hay cinco sólidos regulares.
Toda arista de un sólido regular es compartida por los lados de dos polígonos adyacentes.
Imaginemos de nuevo el cubo en el cual cada arista hace de frontera entre dos cuadrados.
Si contamos todos los lados de todas las caras de un poliedro, nC, habremos contado dos veces todas las aristas.
Por lo tanto C=2A (3)
Sea r el número de aristas que convergen en cada vértice.
En un cubo r=3. T
ambién ahora cada arista conecta dos vértices.
Si contamos todos los vértives, rV, habremos contado del mismo modo dos veces cada arista. Por lo tanto,
rV=-2A ( 4)
Si sustituimos los valores de y C de las ecuaciones (3) y (4), en la ecuación (2) obtenemos la (5):
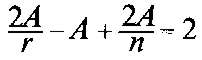
Si dividimos ambos términos de esta ecuación por 2A, tendremos:
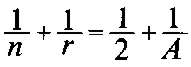
Sabemos que n es 3 o más, porque el polígono más simple es el triángulo, con tres lados.
Sabemos también que r es 3 o más, porque en un vértice dado de un poliedro se encuentran por lo menos 3 caras.
Si tanto n como r fueran simultáneamente más de 3, el primer término de la ecuación(5) seria inferior a 2/3, y la ecuación no podría satisfacerse para cualquier valor positivo de A.
Por lo tanto, y gracias a otro argumento basado en la reducción al absurdo, o bien n = 3 y r vale 3 o más, o bien r= 3 y n vale 3 o más.
Si n=3, la ecuación (5) se convierte en (1/3+(1/r)=(1/2)+(1/A), o bien:
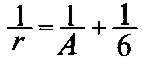
Es decir, que en este caso sólo puede ser igual a 3, 4 o 5. (Si r valiese 6 o más, la ecuación no se cumpliría.)
Ahora bien, n = 3, r = 3 designa un sólido en el cual convergen en cada vértice 3 triángulos.
La ecuación (6) dice que este sólido tiene 6 aristas, la ecuación (3) que tiene 4 caras, la ecuación (4) que tiene 4 vértices.
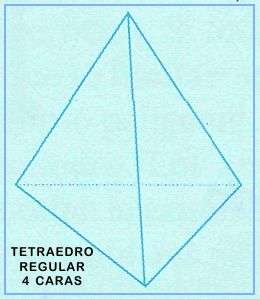
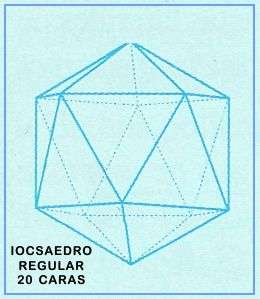
Es evidente que se trata de la pirámide o tetraedro; si n = 3, r = 4 tenemos un sólido con 8 caras en el cual convergen en cada vértice 4 triángulos, el octaedro; y si n = 3, r= 5 tenemos un sólido con 20 caras y con 5 triángulos convergiendo en cada vértice, el icosaedro.
Si r=3, la ecuación (5) se convierte en:
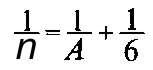
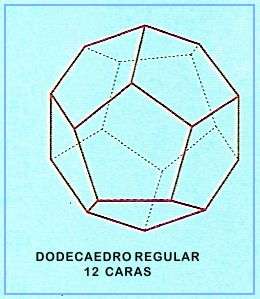
Y utilizando argumentos semejantes n sólo puede ser igual a 3,4 o 5. Si n=3 tenemos de nuevo el tetraedro, si n=4 tenemos un sólido cuyas caras son 6 cuadrados, el cubo, y si n=5 el sólido tiene 12 caras formadas por pentágonos , el dodecaedro.
No hay más valores enteros posibles de n y r por lo tanto sólo hay 5 sólidos regulares, conclusión deducida de la matemática más abstracta y bella , y que como hemos visto tuvo un impacto muy profundo sobre los asuntos prácticos de la humanidad.
Tabla con datos geométricos de los cinco sólidos pitagóricos:
Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Sólo existen cinco de ellos: el Tetraedro, el Cubo, el Octaedro, el Dodecaedro y el Icosaedro.
El nombre del grupo proviene del hecho que los griegos adjudicaban a estos cuerpos cada uno de los "elementos fundamentales": tierra, agua, aire y fuego, y el restante, el dodecaedro, a la divinidad.
Los sólidos platónicos son el inicio del estudio de los poliedros, de estos se derivan los Sólidos de Arquímedes y los de Kepler-Poinsot, que a su vez siguen generando más familias.
El "Mysterium Cosmographicum"
de Johannes Kepler:
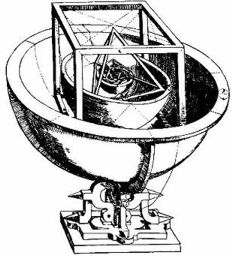
Al edad de 24, Kepler publicó Mysterium Cosmographicum (Misterio Cosmográfico, 1596), en el que defendió la teoría de Copernicus y describió sus ideas en la estructura del sistema planetario.
Influenciado por Pitágoras, Kepler vió el universo como un ser gobernado por relaciones geométricas que conforman círculos inscritos y circunscritos en polígonos regulares de cinco lados.
Centró en los problemas relacionados con las órbitas planetarias, así como en las velocidades variables con que los planetas las recorren, para lo que partió de la concepción pitagórica según la cual el mundo se rige en base a una armonía preestablecida.
Tras intentar una solución aritmética de la cuestión, creyó encontrar una respuesta geométrica relacionando los intervalos entre las órbitas de los seis planetas entonces conocidos con los cinco sólidos regulares.
Juzgó haber resuelto así un «misterio cosmográfico» que expuso en su primera obra, Mysterium cosmographicum (El misterio cosmográfico, 1596), de la que envió un ejemplar a Brahe y otro a Galileo, con el cual mantuvo una esporádica relación epistolar y a quien se unió en la defensa de la causa copernicana.
PLATÓN Y PITÁGORAS: Los Cinco Sólidos Pitagóricos.
Fuente Consultada: Cosmos de Carl Sagan.
Temas Relacionados:
Las Ciencias en Grecia Antigua:Cientificos Griegos
Cientificos Griegos-La Ciencia en Grecia Antigua - Cronologia
Grandes Matematicos Griegos y sus Aportes
Historia de Ciencia Tecnica Tecnologia y Sus Avances
Biografía de Isocrates: Educador en Antigua Grecia y Obra Literaria
Sólidos Platónicos Poliedros Regulares:Demostración de Pitágoras
Demostración pitagórica del número irracional de la raíz cuadrada
Enlace Externo: Sólidos Platónicos – Matemáticas Digitales






