Cinematica: Movimiento Uniforme y Acelerado Ecuaciones Grafica Ejemplos
Cinemática Movimiento Uniforme y Acelerado- Ecuaciones, Gráficas y Ejemplos Prácticos
![]()
TEMAS TRATADOS:
1-Movimiento Uniforme
2-Movimiento Uniformente Acelerado
3-Movimiento Circular Uniforme
4-Gráficas de Velocidad y Espacio
5-Ejemplos
![]()
INTRODUCCIÓN AL MOVIMIENTO:
El concepto de movimiento es la base de la física y se denomina cinemática, del griego kínema, movimiento, nombre que propuso el gran físico francés André Marie Ampére (1775-1836).
Podemos decir con cierta sencillez, que la cinemática se ocupa de determinar la posición de los cuerpos móviles, es decir, dotados de movimiento, en el espacio en función del tiempo; y esto, sin tener en cuenta las causas ni las circunstancias del movimiento.
Puede considerarse, por lo tanto, como una especie de geometría en la que a las tres direcciones del espacio se añade una cuarta, imaginaria, que es el tiempo.
¿Qué es el movimiento?
Es el cambio de posición, respecto a otra que sea o se considere fija (en reposo), y que se toma por referencia, de una figura abstracta (punto, figura plana o sólida invariable) durante un período determinado de tiempo.
El movimiento absoluto no existe; no podemos concebir ni experimentar un movimiento por sí mismo, pero podemos concebir y experimentar movimientos relativos respecto a un sistema de referencia.
Consideramos que un cuerpo situado sobre la superficie terrestre está fijo si observamos que su posición no varía con el transcurso del tiempo, o sea, si su distancia a un punto fijo, por ejemplo, una estaca clavada en el suelo, no cambia.
Pero con el paso del tiempo, el cuerpo y la estaca, la misma Tierra en la que se encuentran ambos, cambia de lugar en el espacio respecto al Sol; y éste, a su vez, también varía de posición, y así sucesivamente.
Sólo que, si pasamos por alto el movimiento de la Tierra (o no lo advertimos), el cuerpo es, para nosotros, inmóvil; mientras que si consideramos el movimiento de la Tierra, el cuerpo es móvil.
Esto significa que, cuando queremos observar y estudiar un fenómeno cinemático, debemos empezar, ante todo, por el establecimiento de una posición de referencia del movimiento, pues de lo contrario no podemos percibirlo ni controlarlo.
Lo que observaremos respecto al movimiento será sólo válido en el ámbito de la referencia; pero será suficiente para la ciencia.
Se pueden, sin embargo, observar movimientos en otros sistemas de referencia y confrontar los distintos resultados, a condición de que se tenga en cuenta el movimiento de los sistemas de referencia uno respecto al otro, o sea, sus movimientos relativos, lo que quiere decir que no podremos nunca disponer de un sistema de referencia privilegiado que sea, en sí mismo y por sí, inmóvil.
De esta consideración partió Albert Einstein para formular la teoría de la relatividad.
El movimiento absoluto no existe porque en el universo no hay nada estático, como para tomarlo como un sistema de referencia especial y único. Por ejemplo cuando me muevo adentro de un colectivo, el mismo se mueve respecto a la calle, pero la calle es parte de la Tierra que se mueve rotando sobre su eje, y a la vez alrededor del Sol.
El sistema solar también se mueve respecto a la galaxia Vía Láctea, que a su vez se mueve respecto a otros sistemas de galaxias, y así seguiremos, sin encontrar un sistema fijo.
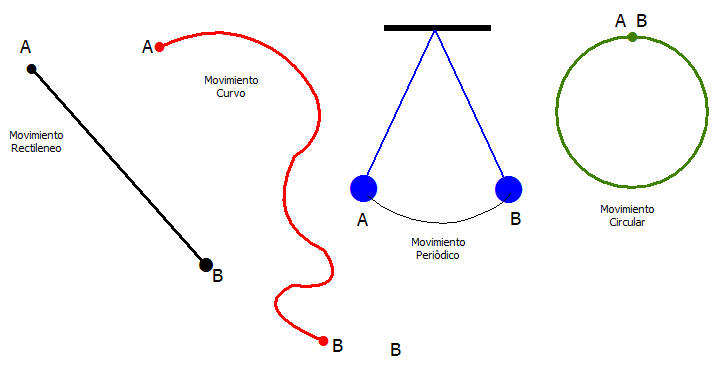
Al pasar, con el tiempo, de una posición a otra, un cuerpo móvil describe una trayectoria que define el movimiento y que puede ser una línea recta, una curva abierta o cerrada, un círculo.
Todos sabemos qué es la velocidad: es el espacio recorrido por un móvil dividido por el tiempo empleado en recorrerlo; si la velocidad de un automóvil es de 100 Km. por hora, significa que en el tiempo de una hora el espacio recorrido será de 100 Km.; y 100 dividido por uno es igual a 100, y la unidad en km./h.
Si hubiésemos tomado el segundo para medir el tiempo, y el metro para el espacio —éstas son, precisamente, las unidades que se emplean en física— la velocidad sería igual a 100 x 1.000 = 100.000; dividido por 3.600, que son los segundos que tiene la hora, el resultado sería 27,77 metros por segundo.
El movimiento puede ser uniforme cuando en tiempos iguales los espacios recorridos son también iguales, o sea, la velocidad es constante.
De otro modo, el movimiento es acelerado si la velocidad aumenta, y retardado si disminuye.
Si la velocidad aumenta en cantidad siempre igual (constante) en cada unidad de tiempo, el movimiento es uniformemente acelerado, y uniformemente retardado en el caso inverso.
Aceleración es la medida de la variación (aumento o disminución) de la velocidad en cada unidad de tiempo.
Si un móvil, a partir de un determinado instante en el que empezamos o al que referimos la medida, recorre 2,50 m en el primer segundo, 3,00 m durante el segundo, 3,50 m durante el tercero, diremos que el cuerpo posee una aceleración de 0,50 m/seg. cada segundo.
Pero estas definiciones, que arrancan de la observación de los movimientos visibles y cuyas características podemos medir directamente, o sea, la forma de la trayectoria, el espacio, la velocidad y la aceleración, están explicados en cualquier libro de Física.
Así, sabemos que existen movimientos periódicos en los que el móvil después de un cierto intervalo de tiempo, llamado período, recupera su posición primitiva y allí empieza en seguida otro movimiento igual al primero.
El ejemplo más sencillo de movimiento periódico es el circular: observemos un punto de la llanta de una rueda de bicicleta, donde está la válvula de la cámara; a cada vuelta volverá a la posición que tenía al principio, y siempre después del mismo tiempo si la velocidad de rotación es uniforme.

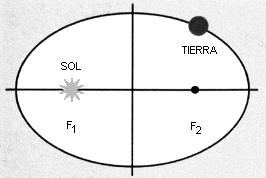
Periódico es también el movimiento de revolución de un planeta alrededor del Sol, aun cuando la trayectoria sea elíptica y la velocidad no uniforme (variada).
También lo son los movimientos oscilatorios como los del péndulo o las vibraciones de las cuerdas tensas y láminas elásticas (movimientos armónicos), en los cuales el movimiento se invierte a cada período.
SÍMBOLOS UTILIZADOS:
En problemas y cálculos relativos a móviles aparecen términos tales como distancia recorrida, tiempo invertido, aceleración constante, velocidad inicial y final.
Puesto que tales términos se usan frecuentemente, es conveniente representarlos por un símbolo.
En realidad, es mejor usar símbolos, porque sin ellos sería casi imposible anotar las fórmulas y las ecuaciones del movimiento.
Estas ecuaciones nos proporcionan un método sencillo de encontrar, por ejemplo, la velocidad final de un móvil, del que conocemos su velocidad inicial, aceleración y distancia recorrida.
Al tiempo se le representa por el símbolo t.
Se mide en segundos. A la distancia recorrida se da el símbolo e. Se mide en metros, o en centímetros.
La velocidad final la representamos por Vi (también se suele usar Vo, ó u), y la velocidad final Vf (se suele usar también V ó v)
Las velocidades se miden en metros por segundo (m./seg.), o centímetros por segundo (cm./seg.).
La aceleración constante se representa por a. Se mide en metros por segundo en cada segundo (m./seg./seg.) o en centímetros por segundo en cada segundo (cm./seg./seg.).

MOVIMIENTO UNIFORME: (M.R.U.)
Concepto de Velocidad y Espacio:
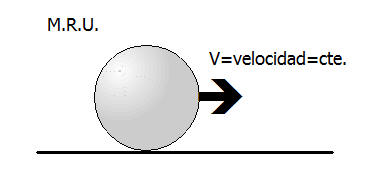
Para estudiar este caso, nos referiremos al movimiento rectilíneo, es decir , aquel que se desarrolla con una trayectoria recta y la velocidad es constate a través del tiempo
Utilizaremos, como cuerpo al que nos referiremos, una pequeña esfera metálica (de hierro, por ejemplo) que representará un punto material, ya que sus dimensiones son pequeñas con respecto a las distancias que vamos a considerar y, entonces, es suficientemente precisa la noción de distancia del cuerpo a un punto, lo cual no sucedería con un cuerpo de dimensiones mayores.
En el caso de la pequeña esfera podemos referirnos a su posición como si fuese la de un punto material.
Esta manera de proceder está justificada, entre otras cosas, por el hecho de que el movimiento de un cuerpo de gran volumen (un auto, un tren una estrella) puede considerarse como el conjunto de los movimientos de todos sus "puntos", es decir, de pequeñísimas porciones en las cuales se lo puede considerar descompuesto.
En el M.R.U. el móvil (nuestra esfera) recorre espacio iguales en tiempo iguales. Así, por ejemplo, puede suceder que un automóvil emplee en ir de una ciudad A a otra B, distantes entre sí 100 Km., el mismo tiempo que tarda en ir de B a C, ciudades que también distan entre sí 100 Km., o sea el automóvil hizo dos recorridos de 100 Km. cada uno en intervalos de tiempo iguales entre sí.
En la realidad si fraccionamos un recorrido dado de 100 Km. en segmentos de 1 Km. cada uno, es seguro que, el automóvil no recorrió cada kilómetro en intervalos de tiempo iguales entre sí (caminos "buenos" y "malos", "aceleradas" para pasar a otro vehículo, disminución de velocidad en cruces, en puentes, etc.), pero para este estudio no nos interesa.
Para un movimiento rectilíneo y uniforme se verifica, entonces, que los segmentos de rectas recorridos en intervalos de tiempo iguales son iguales, cualquiera sea el intervalo.
El espacio recorrido se mide en unidades del metro [m], con submúltiplos y múltiplos, normalmente se usa el milímetro o centímetro para espacio pequeños, y el metro o kilómetro para espacio mas grandes.
Como unidad de tiempo se usa el segundo, minuto y hora.
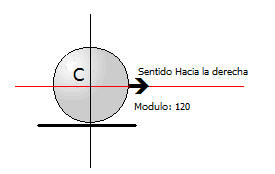
Hay que destacar que la velocidad es una MAGNITUD VECTORIAL, pues tiene punto de aplicación, dirección, sentido y módulo.
EJEMPLO:
Supongamos que el móvil sale del punto A a las 10:33 Hs. y llega al punto B a las 11:00 Hs., recorriendo una distancia entre dos ciudades de 54 Km. ¿Cual es la velocidad del móvil?.
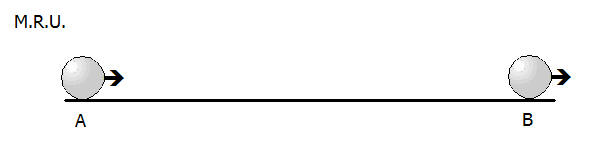
Como decíamos antes seguramente que el móvil ha ido cambiando su velocidad por algún frenado, el pago de un peaje, un control policial, o cualquier inconveniente típico de cualquier viaje.
Para el problema todo eso no nos interesa, solo queremos conocer su VELOCIDAD MEDIA, es decir como si hubiese tenido un viaje ideal entre A y B.
Para este calculo solo debemos tener la distancia recorrida o espacio entre AB, que es igual a 54 Km. y el tiempo empleado que resulta de restar la hora de llegada menos la de partida.
Si lo hacemos es: 11:00 - 10:33= 27 minutos.
Por lo tanto la Velocidad=Espacio Recorrido/Tiempo Empleado
En formula es: V=dE/dT, se dice "delta E" sobre "delta T"
Aplicando la formula es: Vel=54/27=2
La unidad es en el numerador [Km.] y en el denominador [m.], entonces es: 2 [Km.]/[m.], que se lee 2 kilómetros por minuto. Para hallar la velocidad media calculada,por hora se multiplica por 60 minutos que tiene la hora, ósea: 2 . 60 =120 Km. /h.
El vector de velocidad tiene: modulo:120, sentido hacia la derecha, aplicado en C (c.d.g.) y dirección horizontal
Ejemplos de cambio de unidades:

GRAFICAS EN EL MOVIMIENTO UNIFORME:
GRAFICA DEL ESPACIO RECORRIDO EN EL MRU
Ejemplo: un auto sale a las 12:00 de la posición A y a los 2 minutos está en B a 5 Km. de A, luego a los 4 minutos está en C, a los 10 Km. de A y finalmente llega a los 6 minutos después a D, a 15 Km. de A. Hacer la grafica de movimiento antedicho.
Podemos hacer el cuadro siguiente:
| A | B | C | D |
| 12:00 | 12:02 | 12:04 | 12:06 |
| 0 | 5 | 10 | 15 |
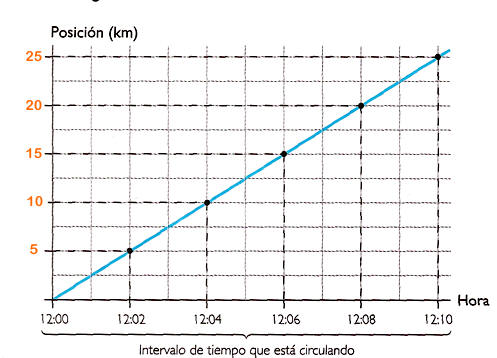
Como el móvil lleva un MRU, podemos seguir con la gráfica y observar que a las 12:08 habrá recorrido 20 Km. y a las 12:10 recorrerá 25 Km.
Obsérvese que recorre espacio iguales en tiempo iguales, cada 2 minutos recorre 5 Km., o cada 4 minutos 10 Km. depende que intervalo de tiempo desea tomar.
De la gráfica también se puede obtener la velocidad, dividiendo el espacio de 5 Km. recorrido por el tiempo empleado de 2 minutos. Vel=5/2=2.5 Km./min. , ósea 150 Km./h.
GRAFICA DE LA VELOCIDAD EN EL MRU
Un móvil se mueve a 27 Km./h. , graficar su velocidad en el tiempo.

Ejemplo: Debemos recorrer 1200 Km. entre dos ciudades A y B. Viajando a 90 Km./h, ¿que tiempo tardaremos en llegar a B?
Sabemos que: e=V.t entonces despejando t=e/V, t=1200/80= 13,33 horas; Los decimales 0,33 es de la hora, entonces multiplicandolos por los 60 minutos de una hora es: 20 minutos. El tiempo empleado será: 13 h 20´

MOVIMIENTO VARIADO:
MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO (M.R.U.A.)
Ante todo digamos que cuando hablamos de movimiento variado, significa que la velocidad del móvil ahora ya no es mas constante como en el caso anterior, sino que la misma va variando con el tiempo.
Por ejemplo un auto sale de reposo (detenido) v1=0 Km./h, acelera hasta lo 40 Km./h en un cierto tiempo, luego continua a esa velocidad hasta llegar a una esquina donde frena levemente para evitar un choque, es decir, que desciende la velocidad a 20 Km./h, para luego volver a acelerar aumentando la velocidad nuevamente.

Como se observa este movimiento es variado, inicialmente acelerado positivamente porque el auto aumenta de velocidad, luego en la segunda etapa se transforma en un movimiento rectilíneo uniforme, hasta la tercera etapa donde frena, es decir ahora el movimiento es acelerado pero negativamente porque el móvil baja su velocidad, finalmente en la cuarta etapa se acelera positivamente otra vez para continuar su viaje.
ACELERACIÓN:
El aumento de velocidad en la unidad de tiempo se denomina aceleración del movimiento variado de que se trate.
El aumento puede ser positivo o negativo, y correspondientemente la aceleración.
Esto da origen a dos denominaciones: movimiento rectilíneo acelerado y movimiento rectilíneo retardado, respectivamente.
En caso de ser la aceleración constante, como en el ejemplo que acabamos de analizar, se tiene un movimiento uniformemente acelerado. En nuestro caso es, además, rectilíneo, ya que su trayectoria es una recta.
Entonces decimos que cuando un objeto aumenta su velocidad se dice que se acelero.
La aceleración del objeto se define como el aumento de su velocidad en un segundo.
Supongamos que un coche marcha a 30 m. por segundo (30 m./s.) y empieza a aumentar su velocidad hasta que, 5 segundos más tarde, va a 40 m. por segundo (40 m./s.). ¿Cuál es la aceleración?
La formula se deduce de la definición anterior, entonces el aumento de velocidad o variación es la velocidad final menos la velocidad inicial, Vf-Vi = dT y se le suele decir "delta T".
Ese dT se divide por el tiempo "t" empleado durante la aceleración, matemáticamente es:
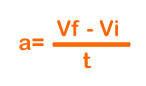
Aplicando esta formula, se tiene un dT de su velocidad es 40 — 30 = 10 m. por segundo. Pero este aumento ha tenido lugar durante 5 segundos; por tanto, el aumento en un segundo es: 10 Km. por hora, dividido por 5 segundos, igual a 2 Km. por hora por segundo.
En otras palabras la aceleración del coche es de 2 m./segundo por segundo, ó bien: 2 m./s²
¿Que significa esta aceleración?,...que el móvil en el 1° segundo pasó de una velocidad de 30 a 32, en el 2° segundo de 32 a 34, en 3° segundo de 34 a 36, en el 4° segundo de 36 a 38 y en el 5° segundo de 38 a 40 m/s.
| Tiempo (seg.) | Velocidad (m./seg.) |
| 0 | 30 |
| 1 | 32 |
| 2 | 34 |
| 3 | 36 |
| 4 | 38 |
| 5 | 40 |
GRAFICA DE LA ACELERACIÓN:
En base al cuadro anterior podemos graficar la velocidad desde el segundo cero (0), en donde la velocidad era de 30 m/seg. y así graficar cada punto de la tabla.
Cuando unimos los valores notaremos que tenemos una recta.
Como el móvil acelera la recta es hacia arriba o con pendiente positiva.
Si el móvil frenara, es decir la velocidad baja en cada segundo, la grafica también seria una recta pero con pendiente negativa o al revés que esta.
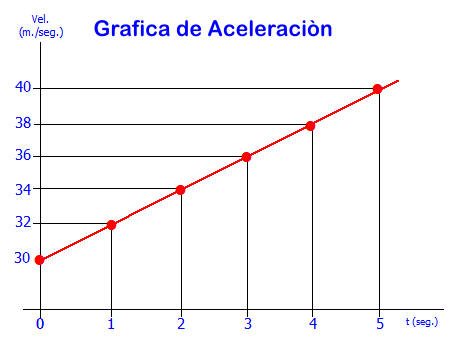
Grafica de la aceleración positiva en un movimiento uniformemente acelerado
La velocidad es la distancia recorrida por un móvil en una unidad de tiempo.
En el caso de automóviles, la distancia se mide en kilómetros y el tiempo en horas, por lo que la velocidad se expresa, generalmente, en Km./hora.
En el laboratorio, las distancias se miden, frecuentemente, en cm. y el tiempo en segundos, en cuyo caso las velocidades se expresan en centímetros por segundo (cm./seg.).
Otro ejemplo de aceleración:
En la figura inicial del auto en movimiento, vemos que frena durante 5 segundo de 40 a 20 Km/h. Cual sería ahora la aceleración?.
En este caso la velocidad final Vf=20 Km./h y la velocidad inicial Vi=40 Km./h, entonces aplicando la formula es: a=(20-40)/5= -20 Km./h/seg., de valor negativo, significa que el móvil viene descendiendo su velocidad, en 20 Km./h cada segundo.
En base a lo anterior también debemos decir que la aceleración (al igual que la velocidad) en una MAGNITUD VECTORIAL, pues tiene punto de aplicación (en el centro de gravedad del móvil), una magnitud (de valor 20), un sentido, hacia la derecha y una dirección que es la del movimiento horizontal del móvil.
Veamos ahora un ejemplo de un ciclista que viaja a 8 m./ seg. y acelera a una velocidad de 1,5 m./ seg.2 durante 10 seg.
¿Qué velocidad alcanzará?
En este problema hay que hallar la velocidad final (Vf), siendo conocidos la velocidad inicial (Vi), la aceleración (a) y el tiempo (t).

Por tanto, hay que usar la primera ecuación de la aceleración, podemos despejar el termino de velocidad final, lo que es:

Los valores conocidos son Vi=8 m./seg., a = 1,5 m./seg./seg., t= 10 seg., y, poniéndolos en la ecuación de arriba, se obtiene v = 8 + 1,5 X 10 = 8 + 15 = 23 m./seg.
Por tanto, el ciclista alcanza una velocidad de 23 m./seg.
¿Cuanto Km./h son 23 m./seg.?, para ello se hace lo siguiente:
Para eliminar los segundo y colocar hora en su lugar, debemos pensar cuanto segundo tiene una hora, ósea 3600 segundos.
Lo mismo para metros, hay que colocar kilómetro en su lugar, entonces, como 1000 metros es un kilómetro, lo colocamos como se indica mas abajo, y se simplifican las unidades m y seg. que son reemplazadas por Km. y h.

EL ESPACIO RECORRIDO EN EL M.R.U.A.
Sigamos con el ejemplo del ciclista, y ahora queremos conocer cual fue la distancia o espacio (e) recorrido por el ciclista durante esos 10 seg. que aceleró a razón de 1,5 m/seg.²
Para hallar el espacio, vimos en el M.R.U. que el mismo es igual a la velocidad por el tiempo, ósea: e=v.t, para este caso en donde tenemos dos velocidades, una inicial Vi y otra final Vf, debemos calcular la velocidad media o promedio , que resulta de sumar ambas velocidades y dividirlas por dos: Vm=(Vi+Vf)/2, entonces es: Vm=(8+23)/2=15.5 m/seg.
Aplicando la fórmula de M.R.U. es: e= Vm. t =15.5 . 10 = 155 m.
Para el M.R.U.A. se puede obtener una fórmula mas general para determinar el espacio recorrido por un móvil, y la misma consiste en hacer los siguientes pasos algebraicos.
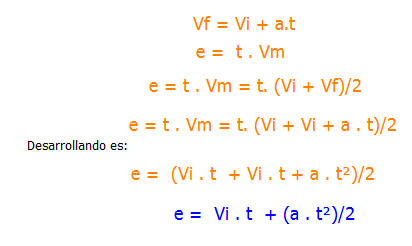
En esta fórmula no hace falta conocer la velocidad Vf, solo depende de la aceleración y la velocidad inicial
Aplicando esta fórmula podemos hacer el mismo problema anterior del ciclista: Entonces: e=8.10 + (1.5 . 10²)/2=80+75= 155 m. , el mismo valor que el hallado anteriormente con la velocidad media.
El espacio recorrido es una ecuación de segundo grado, por lo que su representación gráfica será una parábola, como la que vemos aquí abajo.
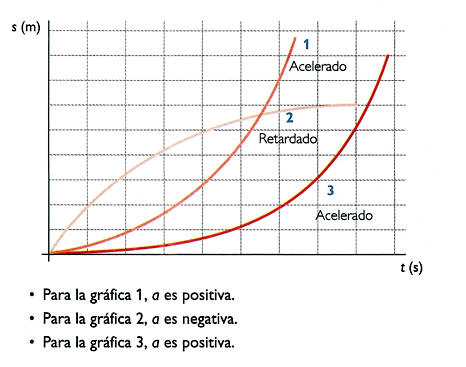
EJEMPLO: ¿Qué espacio recorrerá un camión que avanzaba con una velocidad de 30 m/s si frenó con una aceleración de 3 m/s2?
Los datos del problema son:
Vi=30 m/seg.
Vf=0 , porque si frena se detendrá
a=-3 m/s2 (negativa por viene frenando)
Para aplicar la última formula del espacio, vemos que nos falta el tiempo (t), pero al mismo lo podemos calcular con los datos iniciales del problema.
El tiempo utilizando la definición de la aceleración, de la que ya lo hemos despejado: (Usamos Vo como inicial y V como final)
![]()
Una vez calculado el tiempo que tarda en frenar, sustituimos los datos en la ecuación del espacio (e):
e= Vo. t + (a.t²)/2
e = 30 .10 + (-3 . 10²)/2=300 - 150=150 m.
Observe que al usar la aceleración negativa, el signo de la fórmula del espacio pasa de mas a menos, y se resta un término.
En la gráfica inferior, interpretamos el movimiento realizado por el móvil en cada tramo y calculamos la aceleración en cada uno de ellos.
EJEMPLO: En la gráfica inferior, interpretamos el movimiento realizado por el móvil en cada tramo y calculamos la aceleración en cada uno de ellos.
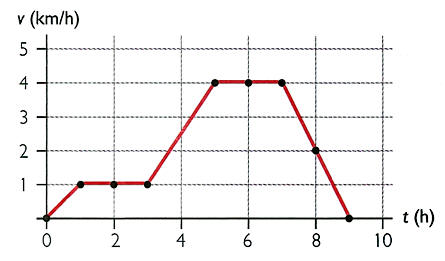
En el Tramo I, aceleró de 0 a 1Km./h en 1 hora , entonces si: a=(Vf-Vi)/2= (1-0)/2= 0,50 Km./seg².
Tramo II, sin aceleración, (pasa el tiempo y no hay variación de a), entonces a=(1-1)/2=0.0 Km./seg²
Tramo III, idem Tramo I, M.R.U.A. (a=positiva) a=(4-1)/2= 3 Km./seg²
Tramo IV, idem Tramo II, aceleración cero.
Tramo V, M.R.U.A., con aceleración negativa, viene frenando, entonces a=(0-4)/2=-2 Km./seg²
ECUACIONES DEL M.R.U.A.
Podemos decir que todos los problemas de cinemática se pueden resolver con las cuatro ecuaciones fundamentales del movimiento y ellas son:

Las dos primeras ecuaciones son, simplemente, la velocidad media y definición de aceleración, usando símbolos en lugar de palabras.
La aceleración a es el aumento de velocidad que tiene lugar en un segundo. En t segundos el aumento de velocidad será, por tanto, at. La velocidad final Vf, después de t segundos, es igual a la velocidad inicial Vi más el aumento de velocidad que tiene lugar en t segundos.
Por tanto, Vf = Vi + a.t, que es la primera ecuación del movimiento. total.
La tercera ecuación resultó de combinar la dos primeras y nos representa el espacio recorrido por un móvil con movimiento acelerado.
Finalmente la cuarta es una gran ecuación, muy utilizada en los problemas que nos relaciona todos los elementos de un problema de cinemática, por lo cual es utilizada frecuentemente.
Podemos obtenerla a partir de la 2°, donde: Vf=Vi+a.t entonces si despejamos t=(Vf-Vi)/a (1)
Sabemos que la velocidad media es: Vm=(Vf+Vi)/2 y como hicimos antes, podemos hallar el espacio recorrido por un móvil en el tiempo t, con la clásica ecuación: e=Vm.t, despejando t=e/Vm (2)
Igualando las t de la (1) y (2) se tiene que: (Vf-Vi)/a = e/Vm
Despejando es: Vm.(Vf-Vi) = e.a
Reemplazando Vm=(Vf+Vi)/2 entonce es: (Vf+Vi) .(Vf-Vi) = 2. a . e
Resolviendo es: Vf²-Vi²=2.a.e ====> Vf²=Vi²+2.a.e (3)
 EJEMPLO: Un vehículo baja a una velocidad de 20 m./seg. y después que ha recorrido 16 metros su velocidad es de 12 m./seg.
EJEMPLO: Un vehículo baja a una velocidad de 20 m./seg. y después que ha recorrido 16 metros su velocidad es de 12 m./seg.
¿Cuál es la aceleración? Se conocen la velocidad inicial (Vi), la final (Vf) y la distancia (e); hay que encontrar la aceleración (a).
La mejor ecuación es la (3), puesto que es la única que no incluye el tiempo (t).
Poniendo en esta ecuación los valores Vi = 20 m./seg., Vf = 12 m./seg., e = 16 m., se obtiene: 12 . 12 = 20 . 20 + 2 .a . 16
144 = 400 + 32 .a
Despejando es: a=(144-400)/32 ====> a=8 m/seg²
La aceleración del vehículo es — 8m./seg².
El signo menos quiere decir que el objeto no está aumentando su velocidad, sino disminuyéndola.
En otras palabras, el vehículo tiene una "retardación" (lo opuesto a una aceleración) de 8 m./seg./seg.
EJEMPLO: Calcular el tiempo que tarda un móvil en recorrer 96 m. si tiene una aceleración de 2m/seg² y su velocidad inicial es de 10 m/seg.
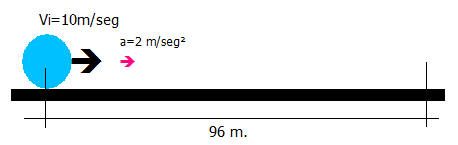
Datos:
Vi=10m/seg
a=2 m/seg²
e=96 m.
Para resolver este problemas debemos recurrir a la ecuación del espacio en M.R.U.A. : e=Vi.t+(at²)/2
La incógnita es t, pero está elevada al cuadrado (t²), entonces debemos recurrir a la resolvente de 2° grado para poder hallar el valor de t.
Armando la ecuación con los datos es: (2.t²)/2 + 10.t - 96=0 (se pasó e restando al otro miembro)
La solución del problema es: t² + 10 t -96 = 0
La forma general de la ecuación de 2° es: at² + bt + c= 0, por simetría es: a=1, b=10 , c=-96
Aplicando la fórmula de la resolvente:
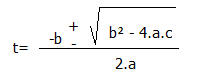
Reemplazando es:
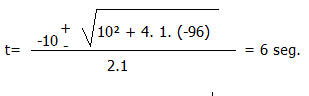
NOTA: Al calcular la resolvente, hallaremos dos valores, por que hay un + - adelante, pero se toma el valor positivo 6, la otra raíz que es negativa se desecha , pues no puede existir un tiempo negativo.
Puede hacer el cálculo online de esa ecuación
MOVIMIENTO CIRCULAR
MOVIMIENTO CIRCULAR UNIFORME (M.C.U.)
En este apartado trataremos de movimientos cuya trayectoria es una curva circular, puede ser una curva completa o vuelta completa y bien una parte o arco de circulo.
Ejemplo sobre este tipo de movimiento hay muchos en la vida real, y los mas comunes son las poleas, las ruedas de los vehículos, las aspas de un molino, una piedra atada a un hilo girando sobre la cabeza de un niño, la rueda gigante de los parques (noria) , en fin hay decenas de ejemplos de movimientos rotatorios.
En nuestro caso estudiaremos el movimiento mas simple, que el uniforme, es decir, que por ejemplo la polea de un motor siempre gira a igual velocidad, digamos 10 vueltas/min.
EJEMPLOS DE MOVIMIENTO CIRCULAR

Polea

Rueda

Rueda de Paque
DEFINICIÓN Observemos el dibujo del margen de abajo. Un objeto que se traslade desde el punto P hasta hasta el punto Q ha recorrido un espacios y ha girado un ángulo Þ (se lee fi), medido en radianes (también se puede medir en °grados). Se puede deducir la expresión del espacio recorrido en metros de una forma muy sencilla.
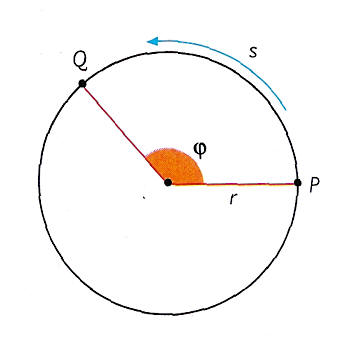 Para una vuelta completa, es decir el perímetro total de la circunferencia de radio r, se tiene que es: 2.Pi.r, donde Pi=3.14
Para una vuelta completa, es decir el perímetro total de la circunferencia de radio r, se tiene que es: 2.Pi.r, donde Pi=3.14
Para una parte de la circunferencia, digamos el arco PQ, simplemente se multiplica el ángulo: Þ.r y se obtiene la longitud del arco s.
Entonces podemos decir que: el espacio recorrido en un movimiento circular uniforme es igual al radio de la circunferencia multiplicado por el ángulo girado, medido este en radianes.
El "radian" es una medida de ángulo y es igual a 57° 18´ aproximadamente, se usa mucho en física porque es mas práctico que usar los °grados sexagesimales. Su equivalencia es muy sencilla
360°=2Pi radianes ó 180°=Pi radianes ó 90°=Pi/2 radianes
Si recurrimos a la formula inicial de M.R.U. donde la velocidad es igual al espacio sobre el tiempo, podemos hallar la velocidad en el movimiento circular, donde el espacio es ahora el ángulo recorrido, para es caso de la figura es:
W=Þ/t
Se llama velocidad angular porque como se observa es el ángulo recorrido por unidad de tiempo.
Si una rueda dá una vuelta por segundo , podemos escribir en radianes asi: 2.Pi rad/seg. porque 2Pi=360°=1vuelta. Si ahora esa misma rueda gira a 5 vueltas por segundo se hace 2.Pi.5=10 Pi rad/seg. Si es 8,7 vueltas por segundo se hace 8,7 . 2 . Pi=17,4 rad./seg.
Si se quiere usar por acostumbramiento el ° sexagesimal , entonces hacemos 5 vueltas por 360°= 1800°/seg., si se tiene decimales hay que calcular cuantos minutos y segundo son esos decimales multiplicando por 60´ y 60´´. Como se ve es mas complicado el cálculo.
LA VELOCIDAD LINEAL:
En el movimiento circular hay dos velocidades bien distintas, y se puede observar cuando una columna de soldados desfilando tienen que doblar en una esquina, en donde el soldado interno de la curva casi no se mueve y el externo (mas lejos del centro) debe acelerar su paso para mantener en orden la columna.
Observe en la figura que el P recorre mas distancia para dar una vuelta que el punto Q, que a su vez este recorre menos que el D.
El caso extremo es el centro C, que no se mueve.
El punto P recorrerá una distancia igual al perímetro de la circunferencia de radio R.
Los mismo para Q y D, pero con un radio menor.
Ya lo hemos calculado, la distancia recorrida por P=2.Pi. R y así para cada punto del cuerpo que gira.
Como el tiempo t en dar una vuelta completa es el mismo entonces se tiene que la velocidad para P será mayor que la velocidad de Q y a la de D.
V=2.Pi.R/t y se la denomina velocidad lineal
(no es mas que el perímetro recorrido por la unidad de tiempo)
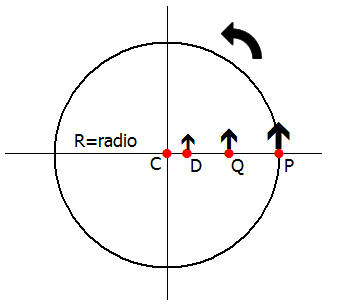
Podemos relacionar muy simple, a ambas velocidades (angular y lineal) a saber:
En la primer figura se sabe que si medimos el ángulo en radianes se tiene que el recorrido s (o arco recorrido) es:
s=Þ.r, dividiendo ese espacio por el tiempo empleado en recorrerlo es: Þ . r / t
pero había definido que Þ/t=W (velocidad angular) entonces reemplazando es:
V=W.r
La velocidad lineal en un movimiento circular es igual a la angular multiplicada por su radio.
EJEMPLOS:
• ¿Qué espacio recorre un móvil que gira un ángulo de 90° sobre una trayectoria circular de 6 m. de radio?
El ángulo girado es: Þ = 90° = Pi/2 rad
Y el espacio recorrido:
s = Pi/2 . r = 6 . 3,14/2 = 9,42 m.
Supongamos que ahora ese mismo móvil recorre 130°, se debe hallar cuanto radianes son, para ello debemos dividir a 130° por (180/Pi), es: 2,269 radianes, que multiplicado por 6 m. se tiene: 13,61 m. recorridos
• Calcular la velocidad angular de una noria que tarda dos minutos en dar una vuelta completa.
t = 2 minutos = 120 segundos
1 vuelta = 2Pi radianes
Sustituyendo los datos en la expresión de la velocidad angular obtenemos lo siguiente: 2.Pi/2= 2. 3.14/120 = 0,05 rad/min. Si se desea saber que ángulo sexagesimal se multiplica 0,05 rad . 57° 18´= 3° aproximadamente
Ley del movimiento en un MCU:
• El movimiento circular uniforme se caracteriza porque:
• Su velocidad angular, w, es constante.
El móvil gira ángulos iguales en tiempos iguales,
El ángulo recorrido es igual a la velocidad angular por t tiempo: W=Þ . t
Se observa que la ley anterior es muy parecida a la ley del movimiento para el MRU: e = v . t
El movimiento circular uniforme es periódico. De una forma regular, el cuerpo vuelve a ocupar la misma posición. Al tiempo que tarda en concluir una vuelta se le llama período (T).
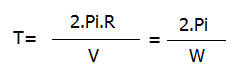
Se llama frecuencia (f) al número de vueltas que da el cuerpo que se mueve en un segundo. Teniendo en cuenta que el cuerpo recorre v metros en 1s, la frecuencia es igual a:
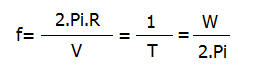
Las unidades que le corresponden a esa magnitud son seg-1 ó Hercios (Hz)
EJEMPLOS:
• Una piedra atada a una cuerda de 0,5 m. de longitud gira a razón de 60 vueltas/minuto.
Calcular:
a) Su velocidad angular en rad/s.
b) El ángulo girado en 5 s.
c) El número de vueltas que dio en ese tiempo.
d) La velocidad lineal de la piedra.
Solución:
a) Como dato sabemos que la frecuencia f=vueltas/minuto, entonces de la fórmula anterior se sabes que: W=f.2Pi
W=60. 2. Pi = 376,8 rad/min ó dividiendo por 60´´ es: 6,28 rad/seg.
b) En ángulo girado es: Þ=W.t reemplazando es: Þ=6,28 . 5 = 31,40 rad.
c) Si dá 60 vueltas/minuto, entonces por segundo es: 1 vuelta/seg. , lo que en 5 seg. girará: 5 vueltas
d) Sabemos que la velocidad lineal es: V=W.R= 6,28 . 0,5 = 3.14 m/s
EJEMPLO:
• La noria de un parque de atracciones tarda 15 seg. en dar una vuelta. Si su velocidad angular es constante, calcular:
a) La velocidad angular en radianes/segundo.
b) El período y la frecuencia.
c) El ángulo girado en 5 segundos.
d) La velocidad lineal de un viajero situado a 10 m del eje de giro.
Solución:
a) La noria se mueve con movimiento circular uniforme, por lo que aplicamos sus ecuaciones.
W=Þ/t ===> 2.Pi/15= 0,13.Pi rad/seg
b) Período es tiempo que tarda en dar una vuelta, entonces el período es: T=15 seg., la frecuencia es la inversa del período, entonces es: f=1/T=1/15=0,06 Hz.
c) El ángulo girado es: Þ= W. t = 0,13 Pi. 5= 0,65 Pi rad=2,04 rad.
d) La velocidad lineal de un viajero es: V=W.R=0,13.Pi . 10= 1.3.Pi=4,04 m/seg.





