Ejemplos de Problemas Matematicos Elementales Para Razonar
Ejemplos de Problemas Matematicos Elementales Para Razonar
Hace unos cuantos años este sitio nació pensando en la difusión de nuestra historia nacional argentina, y la de otros temas históricos que tuvieran alguna relación directa con lo acontencido en nuestro país.
Mas tarde se fueron incrementando poco a poco decenas de nuevos temas , hasta que un día inicié como novedad la publicación de distintos tema científicos pero vistos desde una perspectiva histórica evolutiva.
Los temas científicos son fascinantes y son los cimientos de la evolución tecnológica de la humanidad. Desde aquella primera chispa que generó el fuego, pasando por la maravillosa rueda de los primitivos carros, luego la brujula, la imprenta y hoy los viajes espaciales, es una historia que no deja de sorprenderme y que creo que también a tí te ocurre lo mismo.
Temas tan amplios y cautivadores como la electrónica, la biotecnología, la nanotecnologia , la genética y la informática se han iniciado alguna vez desde un nivel "cero" partiendo de alguna "loca idea" rectora para ir luego sumando nuevos experimentos, investigaciones y descubrimientos.
Lo interesante es que todos ellos tienen algo en común, y es que en todas esas especialidades científicas los primeros pasos se han apoyado en herramientas tan básicas y elementales como las que estudiamos en la primaria y la secundaria.
Ocurre que gran parte de esas herramientas que aprendimos, despúes por alguna razón las hemos dejado en algun rincón de nuestras "cabezas".
La educación es una gran caja de herramientas que luego cada uno utiliza las que mejor se adecuan a sus actividades, pero de todas maneras, a veces no viene mal volver a verlas, a recordarlas o a estudiarlas , aunque sea solo por una curiosidad, o bien para ayudar a nuestros peques que necesitan una mano, o para que nos sirvan a nosotros mismos.
Y de eso se trata este post, que ha sido dividido por ahora en cuatro partes, simplemente por la comodidad para bajar la pagina, pues las cuatro partes son muy similares.
Se plantean una serie de ejercicios básicos sobre temas variados, como geometría, área de figuras, volúmenes de cuerpos, curiosidades matematicas de los números, algunos conceptos físicos como la velocidad, la palanca, o el famoso empuje del gran Arquímedes.
No son problemas de ingenio, ni capciosos, ni rebuscados, solo problemas elementales para razonar juntos un poco, para usar nuestra intuición o pensamiento abstracto y recurriendo a aplicara aquellas herramientas que alguna vez la aprendimos, pero a lo mejor hoy, están olvidadas.
Las primeras fichas son un pequeños repaso simple de conceptos como unidades de medida, potencia, raiz, etc. y luego se presentan distintas cuestiones matemáticas para que intentes pensarla y resolverla.
Todos tienen explicada una solución, también tú puedes presentar otra, porque los caminos en la ciencias son diversos, no importa por donde vayas, mientras que uses las reglas correctamente , cada cual va por el camino que quiere, lo importante el llegar al resultado correcto o aproximado.No todos llegamos de primera a una solución exacta.
Salvando las diferencias, pienso que un ejemplo mas claro de esto, es la actual carrera de decenas de la laboratorios de todo el mundo en que cada uno hace su propia investigación y recorre el camino que mejor le parece para obtener una vacuna eficaz contrar este nuevo virus que nos ha cambiado la vida.
►Unidades de Medidas Mas Comunes
El hombre desde sus primeros pasos en la Tierra debió contar y medir, para contar uso sus dedos y para medir alguna parte de su cuerpo (ver ficha de abajo). Actualmente usamos un sistema llamado Sistema Internacional de Unidades, abreviado S.I., también denominado Sistema Internacional de Medidas, y es el heredero del antiguo sistema métrico decimal, por lo que el S.I. también es conocido de forma genérica como sistema métrico.
Para medir usamos el METRO y sus submúltiplos y múltiplos. En una dirección decimos [metro], en dos dimensines es [metro cuadrado - m²] , y en tres dimensiones [metro cúbico - m³]. Son las medidas de longitud, superficie y volumen.


► Recordando Otras Unidades
Obviamente hay otros sistema de medición, que también vienen de la antiguedad, pero tiene menos uso. Medidas como PIE, YARDA, PULGADA, etc. Lo importante es que recuerdes que 1 pulgada vale: 2,54 cm. o que 1 Pie= 31 cm. (aprox.). Para medir el TIEMPO , usamos un sistema llamado SEXAGESIMAL, es decir cada unidad está dividida en 60 partes. Por ejemplo 1 hora, tiene 60 minutos, y 1 minuto tiene 60 segundos.


►Sumas, Potencia, Area y Perímetro:
Son todos estos (y hay algunos mas) conceptos elementales para que vayas recordando, por ejemplo cuando restas un numero menor a otro mayor y la suma es negativa.
Una forma fácil de entenderlo es pensando que esos números representan dinero, entonces si restas 43 - 50, significa que DEBES 50 Y SOLO TIENES 43 PESOS, LA RESTA SE HACE COMO SIEMPRE PERO COMO QUEDAS DEBIENDO SE COLOCA UN SIGNO NEGATIVO, el resultado es: -7
Vemos también otras unidades como la de PESO Y VOLUMEN. Para el peso usamos unidades como el GRAMO, KILOGRAMO Y TONELADA. Para el volumen se usa (ya hablamos antes) el cm³,dm³,m³...Lo importante es recordar que 1dm³ es igual a 1LITRO, O TAMBIEN 1000 cm³ valen 1 dm³ o 1 litro.
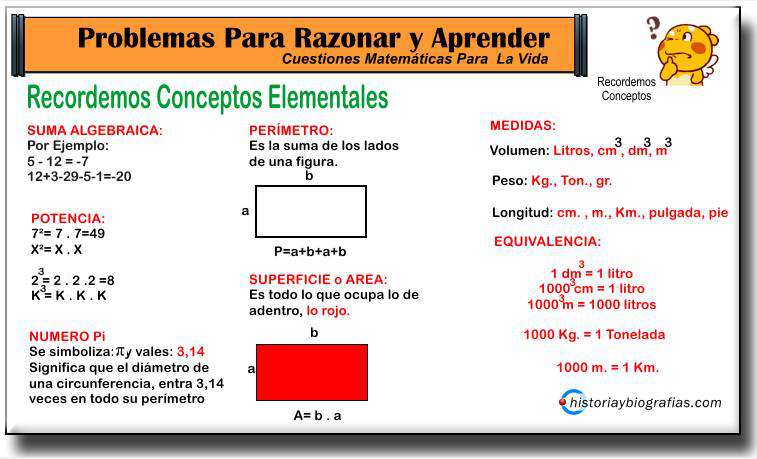

► El Famoso Teorema de Pitágoras:
Seguro que lees Pitágoras y dice de primera el "versito" de su famosa fórmula. En todo triángulo rectangulo los catetos salen (o se unen) siempre en el ángulo recto (90º). La hipotenusa siempre está enfrente de ese ángulo. Una vez que identificas a los catetos y la hipotenusa, simplemente los reemplazas en la fórmula.
Puede ocurrir que como datos tenga el valor de un cateto y el de la hipotenusa, entonces de la fórmula original, debes despejar un término. De esta manera la fórmula será: a²=c²-b² , observa que para hallar un cateto ahora simplemente hay que restar el cuadrado del otro cateto al cuadrado de la hipotenusa. Solo hice un simple pasaje de términos.
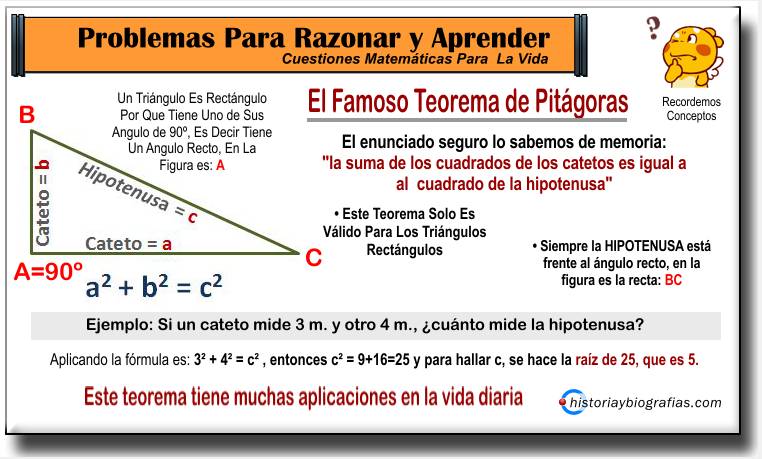

► Area de un Triángulo: Fórmula de Herón
Siempre cuando hablamos del área de un triángulo, sabemos de momoria que es igual a: base por altura dividido 2. Pero muchas veces pasa que no tenemos la altura, entonces podemos recurrir a un gran formula llamada de HERON, que permite hallar la superficie de cualquier triángulo sin conocer su altura. Simplemte se halla su perímetro ( la suma de los tres lados), se lo divide por 2. Esa medida llmada "s" se pone adentro de la raíz. Haz la prueba y verás que es muy simple.
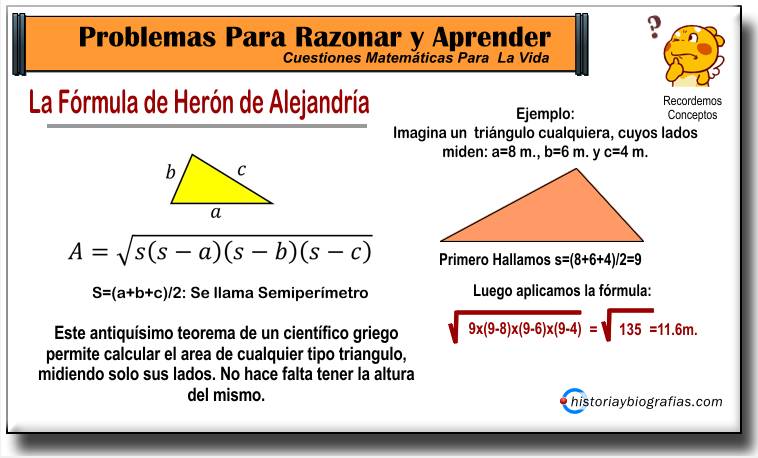

►Perímetro y Area Un Círculo:
Cuando interviene Pi siempre aparecen las confusiones, no?...no hay mucho para hacer, solo memorizar ambas formulitas. El perímetro es igual a PI x diámetro , o también, como el diámetro vale: 2 radios se puede escribir: PI.2.r . Bien ahora para la superficie es PI. r² . Por lo tanto acuerdate que para el perímetro el 2 va a abajo y para la superficie el 2 va arriba.
Problema:


►Cuerpos Simples: Cubo y Esfera
Vivimos en un mundo tridimencional, vivimos rodaados de cuerpos, o de volúmenes, y es común determinar dicho volumen o la superficie lateral de esos cuerpos. Desde niño lo aprendimos en la escuela. La unidad es con el 3 arriba , osea metro cubico, centímetro cúbico, etc. Por ejemplo hallar el volumen de la piscina para determinar los productos a colocarle en su mantenimiento.
Problema:


►Empecemos a Pensar
La idea es aplicar esas fórmulas a nuestro planeta y tener conciencia de lo grande que es y a la vez tratar de memorizar alguna dimension de perímetro o diámetro, que vale casi 13.000 Km.
Problema:


►La Regla de 3 Simple "Directa"
Esta regla, creo que es DE ORO en la vida, porque la vivimos usando, muchas veces la hacemos mentalmente, pero se usa muy seguido. Solo hay que saber si es directa o indirecta, para saber como multiplcamos los valores o los datos. Es directa, si cuando aumentamos o disminuimos una variable, la otra (incognita) también aumenta o disminuye. Por ejemplo si quieres calcular la cantidad de madera para construir varios muebles, y resulta que luego tienes que construir mas muebles, significa que la cantidad de madera también aumentará entonces este calculo de 3 simple es DIRECTO.
Problema:


►Regla de 3 Simple "Indirecta"
Igual que el caso anterior, pero observa bien como se ponen los valores para hallar la X. Lee la ficha , y enseguida lo entenderas.
Problema:


►Regla de 3 Compuesta
Hay un video en youtube que explica en minutos y muy fácil como se hace, aqui tienes el problema explicado para ir pensandolo. También hay que ver si es una relación directa o indirecta, aprender eso y listo, son todos problemas simples. Ver El Video
Problema:


► El Porcentaje:
También todos los días se nos presenta un problema de este tipo, y se resuelve con regla de 3 simple. Sigue este ejemplo para aprender a resolverlo, luego todos los demas porcentajes se obtienen de la misma forma.


►Mas Porcentaje...
Aquí se presenta el cálculo al revés, es decir, tienes el porcentaje y debes determinar cúanto es ese valor. Como regla práctica siempre multiplica el porcentaje/100 por, por ejemplo, el importe o precio del producto. Te dicen 8%, haz 0,08 x precio, te dicen 34%, haz 0,34 por el importe,...Ejemplo: Un TV cuesta 20.000 y te descuenta 15% por pago contado, haz 0,15 x 20.000= 3000 pesos de descuento.
Problema:

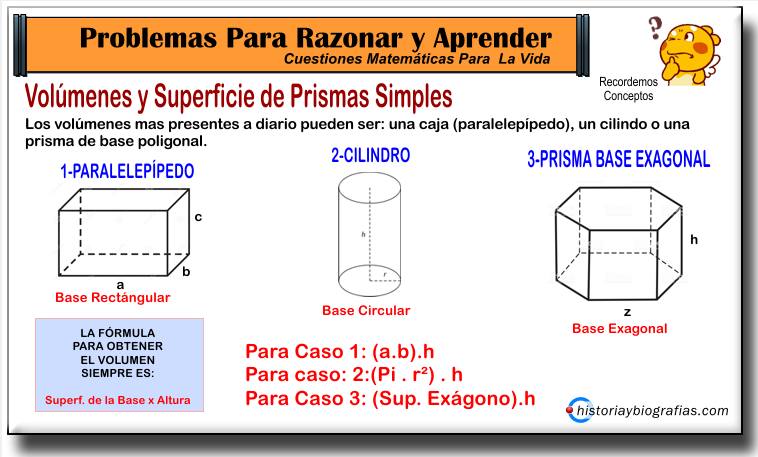
►Volúmenes de Cuerpos Populares
En estos cuerpos regulares, porque tiene una base circular o poligonal (triangulo, cuadrado, rectangulo, pentagono, etc.) la fórmula del volumen SIEMPRE ES LA MISMA, superficie de la base por la altura. Acuerdate que la unidad es cúbica, y es cúbica porque multiplicas tres veces la unidad lineal, por ejemplo [m].[m].[m]=[m³]
Problema:

Este Post Tiene 4 Partes: Parte I - Parte II - Parte III - Parte IV
►La Importancia de la Actividad Cerebral
ENVEJECIMIENTO CEREBRAL:
El envejecimiento puede afectar a la inteligencia fluida, ya que los mensajes entre las células nerviosas se tornan más lentos y, por lo tanto, también es más lento el tiempo de reacción.
La intensidad de la carencia es muy variable.
A medida que transcurre el tiempo, la declinación de la inteligencia puede incluir a más y más personas, pero no las abarca a todas.
Por ejemplo, entre cien personas de cuarenta años, veinte de ellas quizá declinen intelectualmente.
A los cincuenta años, tal vez declinen otras treinta, y así sucesivamente. Pero hay algunas que nunca manifiestan síntomas de decadencia intelectual.
¿Por qué? Es indudable que la salud y los factores hereditarios tienen mucho que ver en ello, pero también influye el sostenido ejercicio intelectual.
En fecha reciente, un grupo de investigadores que trabajan con animales, ha demostrado que el aprendizaje fortalece la transmisión nerviosa y cambia las propiedades físicas de las terminaciones nerviosas.
Tienen la certeza de que lo mismo ocurre con los seres humanos, y que gran parte de las carencias atribuidas a la edad son en realidad la consecuencia de la falta de estímulo de los nervios relacionados con el aprendizaje.
Estudios realizados en el Centro de Investigación de Gerontología del Instituto Nacional del Envejecimiento de Baltimore demuestran que el trabajo intelectual sostenido preserva y mejora las funciones orgánicas de los ancianos.
Si se le enseñan nuevas tretas a un perro viejo, se estimula su funcionamiento mental.
También prolonga su vida. Un estudio realizado a lo largo de doce años con un grupo de sujetos demostró que existe una correlación entre el mantenimiento del vigor intelectual y la capacidad para sobrevivir.
Además, los ejecutivos que realizan tareas que exigen una inteligencia aguda no muestran, al envejecer, los síntomas de debilitamiento del sistema nervioso que se observa en los obreros que envejecen.
Inversamente, cuando se anulan el estímulo y la motivación, la capacidad cognitiva disminuye y hasta puede acortarse la vida.
¿Qué puede usted hacer para mejorar su capacidad de aprendizaje, su memoria y su cognición?
En primer lugar, tenga en cuenta la relación existente entre concentración, atención, estado de alerta, memoria y organización. La concentración es, por definición, la capacidad de centrar el esfuerzo y nuestra facultad mental en un tema.
Cuando usted presta atención, observa y vigila. Cuando está alerta, se halla preparado para entrar en acción. Y cuando organiza, ordena las cosas de una manera sistemática.
Emplea todas las capacidades mencionadas para registrar y evocar recuerdos.
Aunque todavía queda mucho por aprender respecto del almacenamiento y recuperación de los recuerdos, los siguientes ejercicios han demostrado, a lo largo de los años, su efectividad para fortalecer ese sistema maravilloso que empleamos para recordar.
Este Post Tiene 4 Partes: Parte I - Parte II - Parte III - Parte IV
Enlace Externo:• 10 Webs para Resolver Ecuaciones de Matemáticas






