Propiedades de las Raices de una Ecuación Cuadratica
CÁLCULO Y PROPIEDADES DE LAS RAÍCES EN UNA ECUACIÓN DE 2° GRADO
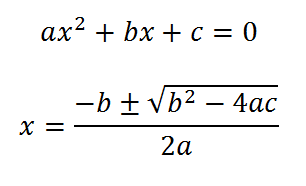
PARTE II: Hola, ¿seguimos sufriendo? .... (VER PARTE I)
Hemos visto la resolución de ecuaciones cuyo coeficiente del término cuadrático es 1, y ahora veremos cómo hacerlo en las que no lo tienen igual a 1.
ECUACIÓN GENERAL
Sea 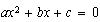 con
con  distinto de 1.
distinto de 1.
Acudiremos al socorrido truco de dividir ambos miembros de la igualdad por el mismo número 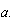 De este modo, obtendremos una NUEVA IGUALDAD, distinta de la anterior, pero que constituye una ecuación EQUIVALENTE a la anterior, es decir, con raíces iguales a las de aquella. (Más adelante, probaremos esta afirmación).
De este modo, obtendremos una NUEVA IGUALDAD, distinta de la anterior, pero que constituye una ecuación EQUIVALENTE a la anterior, es decir, con raíces iguales a las de aquella. (Más adelante, probaremos esta afirmación).
Procederemos:
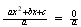 se convertirá en
se convertirá en 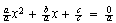 donde
donde 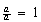
 y
y 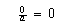
 así que será
así que será 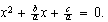
Si ahora aplicamos la "resolvente" (como le dicen los más confianzudos a la fórmula que aprendimos antes), reemplazando
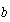 por
por 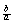 y
y 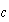 por
por 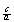 , nos quedará:
, nos quedará: 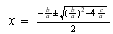 (AB)
(AB)
donde la expresión subradical quedará 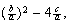 y, entonces, será
y, entonces, será
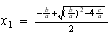 (A) y
(A) y 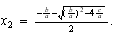 (B)
(B)
Si queremos simplificarnos la vida, podemos efectuar la trasformación de los coeficientes antes de aplicar la fórmula, como en este ejemplo, donde:
 , dividida en ambos miembros por 3, quedaría
, dividida en ambos miembros por 3, quedaría
 que, resuelta como antes aprendimos, daría
que, resuelta como antes aprendimos, daría
 , es decir
, es decir 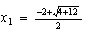 , o sea
, o sea 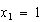
y 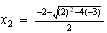 , es decir
, es decir 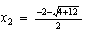 , o sea
, o sea 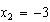
Para estar seguros, reemplazamos la 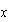 con estos valores en la ecuación original.
con estos valores en la ecuación original.
¿Es 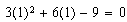 ? Sííí. ¿Y también
? Sííí. ¿Y también 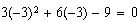 ? Sííí. (¡Qué alivio!)
? Sííí. (¡Qué alivio!)
O bien, podemos buscar una nueva versión de la fórmula para ecuaciones de 2º grado ( recordemos que este nombre implica sí o sí que 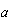 es distinto de
es distinto de 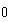 , porque de no serlo no habría término cuadrático, y la ecuación NO sería de 2º grado) que sirva cuando
, porque de no serlo no habría término cuadrático, y la ecuación NO sería de 2º grado) que sirva cuando 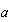 es distinto de
es distinto de 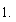
Veamos: Si tomamos (AA), y desarrollamos, tendremos 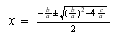

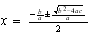 ,
,
y extrayendo denominador común 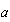 en el numerador y pasándolo al denominador, queda
en el numerador y pasándolo al denominador, queda 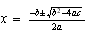
Fórmula que, ahora sí, puede aplicarse a todos los casos de resolución.
Veamos: si 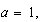 queda la fórmula (AB), que ya estudiamos.
queda la fórmula (AB), que ya estudiamos.
Retomando el caso 2.1 del capítulo anterior, si 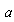 es distinta o no de
es distinta o no de 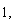 y
y 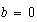 , la fórmula queda como
, la fórmula queda como 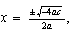 y esto es lo mismo que
y esto es lo mismo que 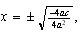 que es lo mismo que
que es lo mismo que 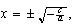 que es lo mismo que habíamos hallado en el punto 2.1 del capítulo anterior.
que es lo mismo que habíamos hallado en el punto 2.1 del capítulo anterior.
Retomemos, ahora, el caso 2.2 del capítulo anterior. Si 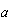 es distinto o no de
es distinto o no de  y
y 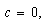 aplicando la resolvente será
aplicando la resolvente será
 que es
que es 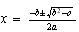 , que es
, que es 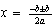
o sea 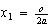 , que es
, que es 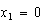 ;
;
y 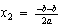 o sea
o sea 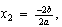 entonces
entonces 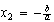 . Que, (¿casualmente?), para el caso de
. Que, (¿casualmente?), para el caso de  son las fórmulas a que habíamos llegado antes.
son las fórmulas a que habíamos llegado antes.
PROPIEDADES DE LAS RAICES DE SEGUNDO GRADO
¿Recuerdan lo que dijimos antes sobre una ecuación expresada como 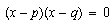 ?
?
En primer lugar, multiplicando los dos factores obtendremos una ecuación de segundo grado,
porque 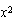
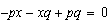 puede expresarse como
puede expresarse como 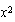
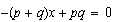 donde podemos asimilar
donde podemos asimilar 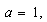
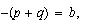 y
y 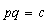 (C)
(C)
Si observamos el primer miembro antes de convertirlo en un polinomio, podemos ver que si 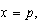 el primer factor es
el primer factor es 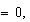 y el producto es
y el producto es 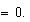
También si hacemos 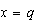 el segundo factor dará
el segundo factor dará 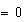 y por lo tanto el producto dará
y por lo tanto el producto dará 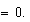
¡ Pero eso quiere decir que 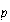 y
y 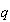 son raíces de la ecuación?????!!!!!!! Y, sí, es así. Y esto nos lleva a varias conclusiones interesantes y útiles.
son raíces de la ecuación?????!!!!!!! Y, sí, es así. Y esto nos lleva a varias conclusiones interesantes y útiles.
1) Una ecuación de 2º grado, conocidas sus raíces 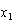 y
y 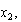 puede expresarse como
puede expresarse como 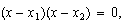 de lo cual se desprende que si no conocemos la forma de la ecuación, pero sí sus raíces, podemos reconstruirla (es decir, expresarla en forma polinómica).
de lo cual se desprende que si no conocemos la forma de la ecuación, pero sí sus raíces, podemos reconstruirla (es decir, expresarla en forma polinómica).
Por supuesto que, de esta forma, siempre obtendremos ecuaciones reducidas, porque si los coeficientes de 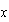 son
son  , el de
, el de 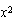 también será
también será 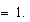
Pero, podemos obtener infinitas ecuaciones de 2º grado, equivalentes a éstas, sólo con multiplicar ambos miembros de la forma factoreada, por cualquier número real.
Por ejemplo, en 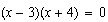 se ve enseguida que
se ve enseguida que 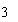 y
y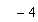 son las raíces, y la forma polinómica sería
son las raíces, y la forma polinómica sería 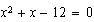 (D) (¿por qué?)
(D) (¿por qué?)
Pero, si multiplicamos ambos miembros, por ejemplo, por 5, la nueva ecuación 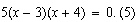 será equivalente a la anterior, porque
será equivalente a la anterior, porque 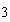 y
y 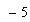 siguen siendo las raíces, y la forma polinómica ahora será
siguen siendo las raíces, y la forma polinómica ahora será
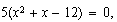 o sea,
o sea, 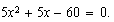
Y así sucederá con cualquier número real por el cual multipliquemos la ecuación reducida.
Ya vimos que si tenemos una ecuación NO REDUCIDA, podemos llegar a la reducida equivalente, dividiendo ambos miembros por el coeficiente de 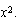
2) Vimos en (C) que , si 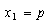 y
y 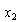
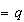 eran las raíces de la forma reducida, entonces, como
eran las raíces de la forma reducida, entonces, como 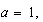
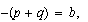 y
y 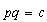 , podemos
, podemos
reconstruir la forma polinómica de la ecuación como 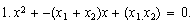
Es decir, que la suma de las raíces, con signo opuesto, es igual al coeficiente del término lineal. O sea 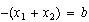
Y el producto de las raíces, es el término independiente. O sea, 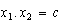 .
.
Podemos verificar que esto se cumple en (D)![$-[3+(-4)]=-(-1)$](https://historiaybiografias.com/graphics/Ec2grado%20P2__100.png)
 , entonces
, entonces 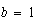 . Y
. Y ![$[3(-4)]=-12$](https://historiaybiografias.com/graphics/Ec2grado%20P2__103.png) , entonces
, entonces 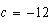 . ¿Y? ¿Qué me cuentan?
. ¿Y? ¿Qué me cuentan?
Pasemos ahora a un tema complejo:
RAICES REALES Y RAICES COMPLEJAS
Si la ecuación es como las que vimos antes, las raíces son números reales, pero si son como, por ejemplo,
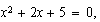 al aplicar la fórmula resolvente tendremos
al aplicar la fórmula resolvente tendremos 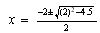 que da
que da 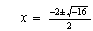
"Pero, ¿qué es esto, Dios mío? ¿Raiz cuadrada de número negativo? ¡Si eso no existe!", dirán algunos. Bueno, no es para tanto. No existe en el conjunto de los números reales, pero para algo se inventaron los números imaginarios, que, asociados con los reales, constituyen los números complejos.
Veamos: Yo sé resolver 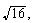 que hasta da raiz exacta y todo, pero,
que hasta da raiz exacta y todo, pero, 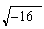 ...
...
Probemos con alguno de los truquitos de los matemáticos. Todos sabemos que es perfectamente legal decir que
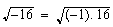 y, como la buena de doña Propiedad Distributiva de La Radicación Con Respeto A La Multiplicación nos lo permite, decimos con toda tranquilidad de conciencia que
y, como la buena de doña Propiedad Distributiva de La Radicación Con Respeto A La Multiplicación nos lo permite, decimos con toda tranquilidad de conciencia que
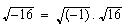 o sea
o sea 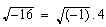 .
.
Con lo cual hemos solucionado la mitad del problema. Pero, ¿qué cosa exótica es ese 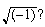 . Pues es
. Pues es 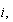 la unidad imaginaria que fue inventada justamente para estas situaciones críticas.
la unidad imaginaria que fue inventada justamente para estas situaciones críticas.
Esta unidad no se define como 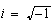 sino como el valor que cumple
sino como el valor que cumple 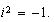 Pero, en la práctica, sirve justamente para operar con
Pero, en la práctica, sirve justamente para operar con 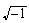 reemplazándolo cuando aparece para fastidiar. Por otro lado, observemos que (
reemplazándolo cuando aparece para fastidiar. Por otro lado, observemos que (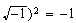 , así que no es incorrecto hacer esa sustitución.
, así que no es incorrecto hacer esa sustitución.
Visto todo lo cual, volvemos a nuestra ecuación, donde las raíces serán
 o sea
o sea 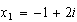 , y
, y
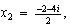 o sea
o sea 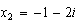
Si miramos fijamente a los dos valores obtenidos para las raíces, veremos que son casi iguales, salvo por el signo de los términos que contienen a 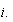
Son números complejos, porque constan de una parte real :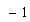 , y una parte imaginaria:
, y una parte imaginaria: 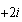 uno, y el otro
uno, y el otro 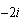 . Son lo que se llama, dos números complejos conjugados, es decir que tienen las partes reales iguales, y las partes imaginarias opuestas (de igual valor numérico y distinto signo).
. Son lo que se llama, dos números complejos conjugados, es decir que tienen las partes reales iguales, y las partes imaginarias opuestas (de igual valor numérico y distinto signo).
Y siempre que una ecuación tenga raíces complejas, serán números complejos conjugados, porque la parte real es igual y la imaginaria proviene de raices iguales, pero precedidas por distinto signo.
Reemplacemos ahora, en la ecuación en cuestión, a 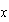 por los valores hallados, para comprobar que estas raíces son las correctas (es decir, comprobaremos que realmente es una igualdad). Mientras no lo demostremos, lo escribiremos como pregunta
por los valores hallados, para comprobar que estas raíces son las correctas (es decir, comprobaremos que realmente es una igualdad). Mientras no lo demostremos, lo escribiremos como pregunta
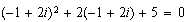
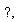 Podemos pensar el primer miembro como
Podemos pensar el primer miembro como 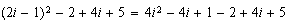 , donde los términos en
, donde los términos en 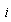 se anulan mutuamente, y reemplazamos
se anulan mutuamente, y reemplazamos 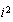 por
por 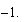
Será, entonces, 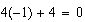 . Así que para la primera raiz, ya estamos cumplidos.
. Así que para la primera raiz, ya estamos cumplidos.
Para la segunda, reemplazamos y resolvemos 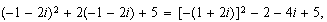 o sea
o sea
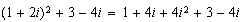 (después de desarrollar el cuadrado del binomio) donde también se anulan los términos con
(después de desarrollar el cuadrado del binomio) donde también se anulan los términos con 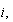 y es
y es 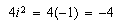
O sea, 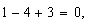 que es lo que queríamos comprobar, también para la segunda raiz.
que es lo que queríamos comprobar, también para la segunda raiz.
¿Y qué generalización podríamos extraer de esto? Podríamos observar que esta situación se da cuando la expresión subradical es negativa, es decir 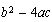 es menor que 0, es decir que
es menor que 0, es decir que 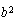 es menor que
es menor que 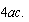
Entonces, sólo con ver la forma de la ecuación estaremos en condiciones de predecir si las raíces serán complejas o reales.
En nuestro ejemplo, se ve enseguida que 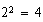 es menor que
es menor que 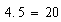 .
.
Y, para terminar, por hoy, les dejo unas cuantas ecuaciones para resolver, con sus respectivas soluciones, para mirar DESPUES de resolverlas, no antes. También les propongo un problema que se resuelve utilizando ecuaciones.
Aquí van:
Hallar las raíces de : 1) 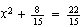
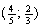
2) 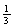
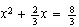
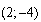
3) 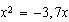
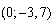
4) 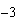
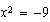
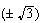
5) 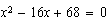
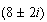
Problema: Un móvil parte de A con movimiento rectilíneo uniformemente acelerado. Sale con una velocidad de 3 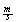 y al cabo de 10 segundos su velocidad es de 7
y al cabo de 10 segundos su velocidad es de 7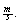 ¿Qué tiempo deberá trascurrir para que recorra 18900 m desde su punto de partida? (Solución: 5 minutos)
¿Qué tiempo deberá trascurrir para que recorra 18900 m desde su punto de partida? (Solución: 5 minutos)
(Algunas aclaraciones:
1) la fórmula para calcular la distancia en un movimiento de este tipo es 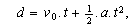 donde
donde 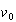 es la velocidad inicial,
es la velocidad inicial, 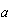 es la aceleración, y
es la aceleración, y 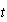 el tiempo,
el tiempo,
2) la aceleración es el incremento de la velocidad dividido por el tiempo que duró ese incremento, y
3) en los problemas de física, sólo se tendrá en cuenta el valor positivo entre los hallados como solución.)
Bien, hasta la vista, amigos.
Las propiedades de las raíces de una ecuación de 2º grado.
Calculo Online de las Raíces de Un Función Cuadrática
"Silvia Ele, la autora de esta colaboración, es una profesora de matemática de muchos años, con quien podés comunicarte enviándole un mensaje a [email protected] "






