Maquinas Simples:Tipos de Palancas,Poleas, Plano Inclinado,Ejemplos
Máquinas Simples: Tipos de Palancas, Poleas, Plano Inclinado
TEMAS TRATADOS:
1-Concepto de Máquina Simple
2-Palancas, Tipos ó Géneros, Ejemplos
3-Las Poleas, Tipos
4-Torno, Multiplicación
5-Plano Inclinado, Multiplicación
Ver: Concepto de Momento Flector Aplicado a Palancas
► ¿Que son las máquinas simples?:
¿Qué es una máquina?: Una batidora de huevos, un gato de automóvil, un aparejo de poleas, una rampa de carga .. . son todos máquinas.
¿Qué tienen precisamente en común? O dicho en otras palabras, ¿qué es una máquina?.
Una máquina es un dispositivo mecánico que permite trabajar más cómodamente, aumentando la velocidad de una operación, o disminuyendo la fuerza que debe aplicarse, o cambiando la dirección de la fuerza.
Es más fácil batir un huevo con una batidora que con un tenedor, porque puede hacerse que las cuchillas se muevan más rápido que el tenedor.
Sería imposible para la mayoría de la gente levantar el eje posterior de un carro de modo que pueda cambiarse una llanta; con un gato, hasta un niño puede hacerlo.
Una máquina no es una fuente de energía, para que trabaje se le debe suministrar energía: hacer girar la manivela de la batidora de huevos o mover la palanca del gato.
El trabajo mecánico realizado sobre una máquina se llama trabajo suministrado; y el trabajo mecánico efectuado por la máquina sobre algún otro cuerpo se llama trabajo ejecutado.
Con el gato de automóvil, por ejemplo, el trabajo suministrado en cada empujón a la palanca, es igual a la fuerza que se ejerce multiplicada por la distancia que avanza la mano.
El trabajo ejecutado es el peso levantado, multiplicado por la altura que se eleva.
Hay muchas clases de máquinas simples.
Pero en Física, como en cualquier ciencia, el problema se simplifica agrupando todos los dispositivos análogos.
Cuando esto se lleva a cabo, muchas máquinas simples pueden clasificarse en dos grupos: planos inclinados y palancas.
Las palancas, poleas, tornos y planos inclinados se denominan máquinas simples, y no obstante haber sido inventadas hace miles de años, todavía reportan gran utilidad.
En cualquier tipo de las máquinas que se usan actualmente, aun las más complicadas, no existen sino combinaciones más o menos ingeniosas de una o más máquinas simples.
No hay más que observar una máquina de escribir o una máquina de ferrocarril: por todos lados descubriremos palancas, tornos, poleas, engranajes, etc.
En esta página estudiaremos varias máquinas simples.
El objeto de nuestro estudio puede sintetizarse así:
1) Qué fuerza es necesaria para mantener en equilibrio a un cuerpo, empleando una máquina simple.
2) Cuánto vale la multiplicación de cada máquina, es decir, por cuánto se multiplica nuestra fuerza al emplear la máquina.
1-MAQUINAS SIMPLES: PALANCAS
Una palanca es, en general, una barra rígida, que puede girar alrededor de un punto o de un eje.
Para alzar la esfera por medio de una palanca es más conveniente proceder como en (a); si ejercemos fuerza más cerca del punto de apoyo, será necesario un esfuerzo mayor (b).
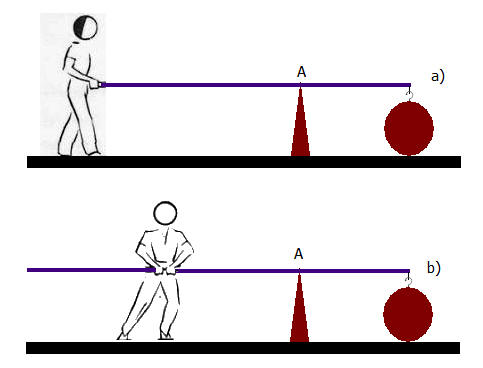
Imaginemos que se trata de levantar un peso, como está indicado en la figura.
Instintivamente trataremos de tomar la palanca lo más lejos posible del punto de apoyo A, pues sabemos que así es más fácil levantarlo.
Si tomamos la palanca por la mitad, habrá que hacer más fuerza, y aun así es posible que no lo podamos levantar.
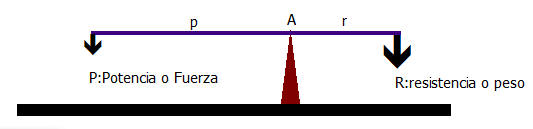
Esquema físico de la palanca
La explicación es evidente: el peso que queremos vencer, que llamaremos resistencia R, tiende a hacer girar la palanca en el sentido señalado.
Es decir, constituye una cupla de momento R . r respecto de A; la fuerza aplicada para vencerlo, que llamaremos fuerza motriz P, constituye una cupla de momento P p.
La condición para que un cuerpo sometido a cuplas esté en equilibrio, es que la cupla resultante tenga momento nulo.
Como en este caso las fuerzas son paralelas, sus vectores-momento tienen la misma recta de acción, y para que el momento resultante sea nulo deberá ser:
M (P) + M (R) = 0.
La condición para que una palanca esté en equilibrio es que la suma de los momentos de la fuerza motriz y de la resistencia, con respecto al punto de apoyo, sea nula.
Ahora bien, podemos escribir el equilibrio de una palanca como: P.p = R.r
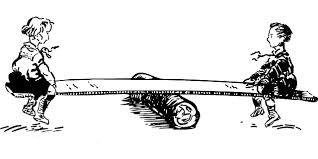
El ejemplo mas simple es el juego de niños subibaja, donde las distancias r y d son iguales y si los pesos son también parecidos el mismo quedará horizontal.
Cuando uno de los niños se aleja del apoyo o es mas pesado enseguida la tabla se inclina hacia un lado porque la ley de equilibrio de momentos o cuplas ya no existe.
EJEMPLO GENERAL: Se tiene una palanca de 1.0m. de largo, y se quiere levantar un peso de P=200Kg, apoyando la barra a r=0,20m. del apoyo. Cual es la fuerza P que debemos realizar para este caso.

Solución: Aplicamos la fórmula general de palanca y reemplazamos los valores datos del problema:
P.p = R.r
P.0,80 = 200.0,20
P=200.0,20/0.80=50 Kg.
Factor de Multiplicación de una Palanca: R=P.p/r
es decir, que la palanca multiplica a la fuerza motriz por el factor d/r llamado factor de multiplicación. Así, si el brazo de la fuerza motriz es 4 veces mayor que el de la resistencia (80 cm : 20 cm = 4), cualquier fuerza que se aplique en A' aparecerá en A" multiplicada por 4.
• TIPOS DE PALANCAS
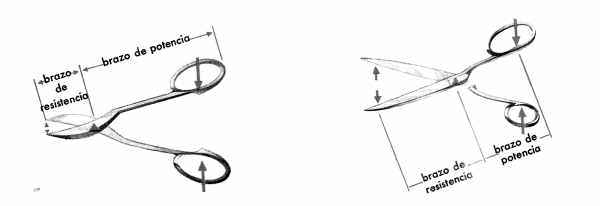
Son palancas de primer género aquellas cuyo punto de apoyo está entre la resistencia y la fuerza motriz. Ejemplos.- las tijeras, las balanzas de platillos, el subibaja.
Palancas de segundo género son aquellas que tienen la resistencia aplicada entre el punto de apoyo y la fuerza motriz. Ejemplos: la carretilla, el rompenueces.
Palancas de tercer género son aquellas que tienen la fuerza motriz entre el punto de apoyo y la resistencia. Ejemplos: el pedal de la máquina de afilar, las pinzas para servirse azúcar.
Cualquiera que sea el género de palanca, la condición de equilibrio es la misma: P.p=R.r

Incluso las máquinas más complejas son combinaciones de máquinas simples.
Arquímedes fue el fundador de la estática. Fue físico, matemático, inventor e ingeniero militar.
Con sus aparatos mantuvo a raya a los romanos durante mucho tiempo, y cuando por fin las legiones consiguieron entrar en la ciudad, dieron muerte al sabio.
La leyenda que se ve arriba dice en latín: "Tócalo y lo moverás".
Se ve, en efecto, que un señor con barba apoya con gran delicadeza un dedo sobre el extremo de la palanca y levanta la Tierra.
Ya hemos visto que con un brazo de fuerza motriz suficientemente largo, un hombre puede levantar cualquier peso. Claro que necesita un punto de apoyo.
Arquímedes decía, según es fama: "Dadme un punto de apoyo y moveré la Tierra".
En el grabado, el punto de apoyo es una gran mano que emerge misteriosamente de entre las nubes.
------------- 00000 ------------
• PALANCA DE 1° GENERO O TIPO
• PALANCA DE 2° GENERO O TIPO
• PALANCA DE 3° GENERO O TIPO
------------- 00000 ------------
Ejemplos Prácticos de Palancas
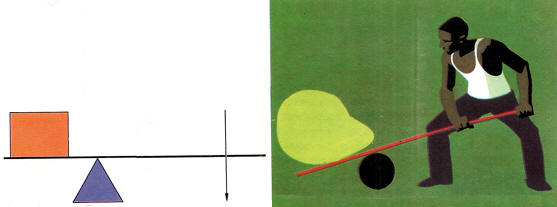
a. Las tijeras de hojalatero y las tenazas están hechas con un par de palancas. La fuerza que realiza el corte es mayor que la fuerza que se ejerce en los mangos. b. La ventaja mecánica de estas tijeras, es mayor que 1 al iniciarse el corte y se vuelve menor que 1 cuando el corte tiene lugar donde están las flechas sobre las cuchillas.

c. Un cascanueces es un par de palancas con el fulcro en un extremo. Nótese cómo se miden aquí los brazos de la potencia y de la resistencia.d. Las pinzas también tienen el fulcro en un extremo pero las posiciones de las fuerzas de la potencia y de la resistencia están invertidas.
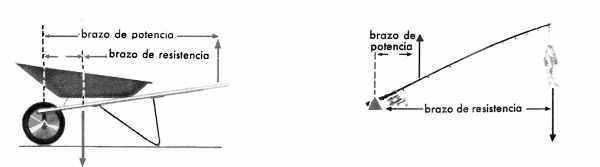
e. Una carretilla tiene un brazo de potencia mayor que el de la resistencia y, por tanto, una gran VM.
f. Una caña de pescar tiene una ventaja mecánica menor que 1, lo que hace posible mayor rapidez de movimiento en el extremo de la resistencia.
------------- 00000 ------------
► Ejemplo de Una Palanca
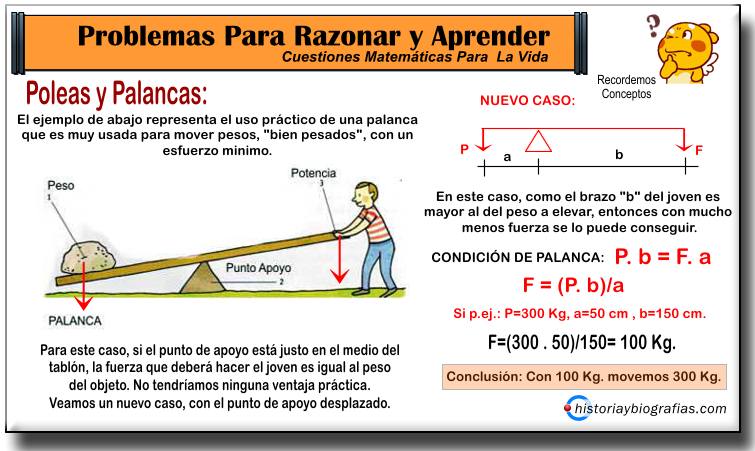
Este señor levanta una piedra pesada, de 100 Kg. con solo 25 Kg. de su propio esfuerzo, pero observa que el brazo de palanca es de 120 cm. mucho mas largo que el de la piedra que es 30 cm. El hombre tiene un brazo de palanca 4 veces superior, por lo que su esfuerzo para levantar el peso será 4 veces inferior (100/4=25 Kg.)

Aplicando la física, se tiene como condición de una palanca que:
El Momento positivo = Al momento negativo
30 cm. x 100 Kg. =120 cm. x potencia
3.000 Kg. = 120 x potencia ====> potencia=25 Kg.
ventaja mecánica = 100/25= 4
Al usar esta palanca, la potencia requerida se reduce a la cuarta parte de la que se necesitaría para levantar la piedra directamente del suelo.
------------- 00000 ------------
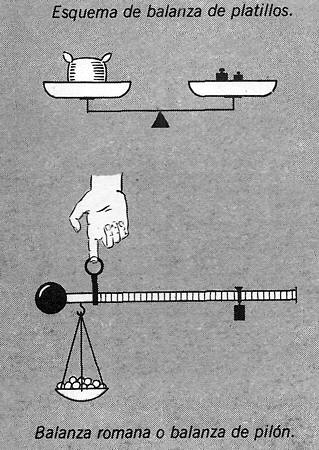
• PALANCAS: BALANZAS
Las balanzas son una aplicación de la palanca.
Hay diversos tipos: pero las más comunes son las de platillos y la romana o de pilón.
Las primeras son palancas de brazos iguales, de modo que la resistencia y la fuerza motriz deben ser iguales.
En las romanas, en cambio, el brazo de la resistencia es siempre menor.
Algunas de éstas tienen dos lugares de donde colgar la resistencia: el más cercano al punto de apoyo se usa cuando la resistencia es muy pesada. ¿Porqué?
• Balanza de precisión.
Es una palanca de brazos iguales; el eje de donde penden los platillos se llama cruz, y todos los apoyos están construidos de manera de disminuir al mínimo los rozamientos.
El fiel, solidario con la cruz, señala en una escala su posición, pero no indica el peso.
Para pesar un cuerpo se siguen procedimientos especiales, que permiten medir pesos de hasta 0,1 mg. con toda facilidad.
Estas balanzas son comunes en todos los laboratorios.
Como son muy delicadas, se las mantiene en una caja de vidrio, dentro de la cual se realiza la pesada, para evitar que las corrientes de aire influyan en la operación.
Se han construido balanzas mucho más precisas que las corrientes de laboratorio.
Con una de ellas se ha tenido la curiosidad de pesar el punto gramatical que se coloca al final de cada oración: pesa 0,000001 gr. también se ha pesado un granito de arena tomado de una playa de mar, que pesa 18 veces más: 0,000018 gr.
EL TORNO:
El torno no es sino una palanca con forma apropiada para que dé muchas vueltas y pueda arrollar una soga. Lo constituye un cilindro que por medio de una manija gira alrededor de su eje, que permanece fijo.
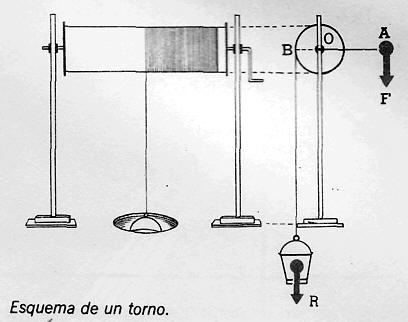
La figura muestra un torno: el circulito en O es la proyección del eje; el círculo da radio O B es la sección del cilindro, y O A es el brazo de la manija.
La condición de equilibrio del torno es la misma que la de la palanca: que la suma de los momentos de las fuerzas aplicadas sea nula:
M (P) + M (R) = 0
Ósea:
F. OA = R .0 B
• MULTIPLICACIÓN DEL TORNO
De la condición de equilibrio: R=F. OA/OB
El factor OA/OB es la multiplicación del torno. Si, por ejemplo, la manija tiene 40 cm de largo y el radio del cilindro mide 10 cm, la multiplicación vale 40 cm: 10 cm = 4. Cualquier fuerza que se aplique en la manija aparece en la periferia del cilindro multiplicada por 4.
2-MAQUINAS SIMPLES:LAS POLEAS:
Las poleas hacen posible que un hombre levante objetos de varias veces su propio peso. La misma acción de agacharse para levantar algo es incómoda y por cierto dificultosa si el objeto es pesado.
Es mucho más fácil levantar el objeto tirando del cable de una polea. Así, los músculos del hombre funcionan más eficientemente y la posición erecta es ciertamente mucho más cómoda.
La polea más sencilla consiste en una rueda acanalada suspendida por su eje del cielo raso y que puede girar libremente. Se le dice polea fija porque está fijada al cielo raso. Alrededor de la rueda pasa un cable o una cadena.
Un extremo se asegura a la cosa a levantar, del otro extremo se tira para levantarlo. Aquí el único beneficio es el de la postura, ya que puede ejercerse el esfuerzo en posición erguida. Pero para levantar 50 Kg. debe ejercer un esfuerzo de por lo menos 50 Kg. La ventaja mecánica de este dispositivo es de uno.
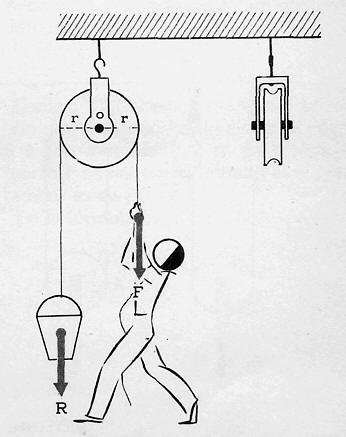
Polea Fija
La carga (resistencia) es igual al esfuerzo (potencia). En la práctica se utilizan sistemas de poleas cuya ventaja mecánica es superior a uno, es decir, que permiten elevar cargas mucho mayores con el mismo esfuerzo.
Aplicando la condición de equilibrio de una palanca:
P.p=R.r
Como p=r, entonces P=R
Es decir la fuerza es igual al peso a levantar
Hay ciertas combinaciones o disposiciones de armar un sistema de poleas que con un esfuerzo de 25 Kg. una persona puede levantar un peso de 50 Kg., y en ese caso decimos que el sistema de poleas posee una ventaja mecánica o factor multiplicador de 2.
Si con un esfuerzo de sólo 10 Kg. pudiéramos levantar una carga de 50 Kg., la ventaja mecánica sería de 5.
Hay un disposición en donde una polea móvil simple puede dar una ventaja mecánica de 2.
En este caso, un extremo del cable es fijo y la polea, de la cual está suspendida la carga, sube junto con ella al tirar nosotros del otro extremo del cable.
Como la carga está suspendida de dos lados, cada uno de los cuales toma la mitad del esfuerzo, éste se reduce a la mitad.
A primera vista esto parece ser un medio de conseguir algo por nada, pero, en realidad, no es así.
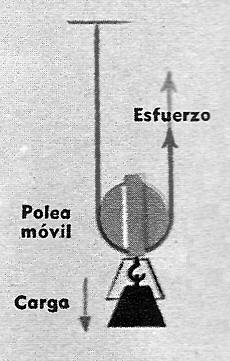
• EXPLICACIÓN:
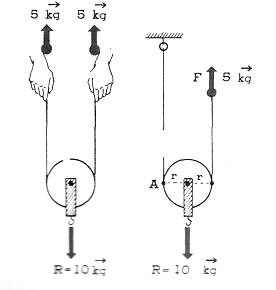
En lugar de apoyarse en el eje como la fija, lo está en la cuerda. Para equilibrar una resistencia R, se aplica la fuerza F (se usa F en lugar de P); estudiaremos ahora qué relación hay entre ambas fuerzas.
La figura muestra que para equilibrar 10 Kg., cada mano debe aplicar 5 Kg.; si nos desentendemos de una de las ramas, atándola al soporte, la fuerza motriz aplicada es de sólo 5 Kg.
Siempre será, pues: F=R/2 , para este caso, la condición para que una polea móvil esté en equilibrio es que la fuerza motriz sea la mitad de la resistencia.
La explicación es sencilla: si observamos una polea móvil en funciones, veremos que la rotación se produce alrededor del punto A. Para que esté en equilibrio, la suma de los momentos de la fuerza motriz y de la resistencia debe ser nula:
M(F) + M(R)=0
P . p = R . r
M (F) = F . 2 r (r, radio de la polea)
M (R) = - R . r
F. 2r- R.r = 0 ==> F= R/2
• MULTIPLICACIÓN DE LA POLEA MÓVIL:
En el caso de fuerzas paralelas: R = 2F La multiplicación de la polea móvil es 2.
El trabajo hecho por el esfuerzo jamás es menor que el aplicado a la carga. Lo que ocurre es que por cada metro de cable que tiramos la polea sube solamente 50 cm., puesto que los cables por acortar son dos.
Es decir, en la polea móvil la potencia debe moverse una distancia dos veces mayor que la resistencia.
Decimos que su relación de velocidades es 2 distancia recorrida por el esfuerzo distancia recorrida por la resistencia Si las poleas no tuvieran peso propio y no existiera fricción, que se opone al movimiento, la ventaja mecánica y la relación de velocidades serían iguales.
Pero en la realidad existe el frotamiento y la polea pesa algo, de modo que se necesita un esfuerzo adicional para vencer estas resistencias.
En la práctica, esto disminuye la ventaja mecánica, que es menor que la relación de velocidades. Aquí, para simplificar, las poleas se suponen sin peso ni fricción.
Un aparejo consiste en una combinación de poleas fijas y móviles dispuestas de modo que se pueda levantar un peso tirando cómodamente en posición erguida, hacia abajo.
Una manera rápida de determinar la ventaja mecánica en aparejos como los ilustrados, llamados factoriales, es contar el número de cables que sostienen la carga. Si hubiera cinco cables, la ventaja mecánica sería entonces de cinco.
3-MAQUINAS SIMPLES: EL PLANO INCLINADO
Una máquina tiene por objeto utilizar ventajosamente energía para producir trabajo. En general, la máquina proporciona un modo más fácil de hacer el trabajo, pero en ningún caso se puede conseguir de la máquina más trabajo que el que se le, suministra.
Artículos anteriores sobre palancas y poleas han demostrado que es posible, en comparación, levantar grandes pesos mediante la aplicación de fuerzas pequeñas.
El plano inclinado es otro medio para levantar un gran peso con facilidad. Es especialmente útil para cargar barriles y toneles, puesto que se pueden rodar hacia arriba por la pendiente.
Este método se usa, actualmente, para cargar barriles de cerveza en carros y camiones de reparto, pero hace tiempo se utilizó mucho más ampliamente.
El plano inclinado debe de haber sido una de las pocas máquinas que el hombre tenía en la antigüedad. Por ejemplo, los primitivos egipcios utilizaron las pendientes en gran escala para la construcción de las pirámides.

Ejemplo simple y que nos trae recuerdos, el tobogán es un plano inclinado, que nos permite deslizar suavemente desde una altura importante que de otra manera nos lastimaríamos. Cuánto mayor es el ángulo en el piso más rápido descendemos porque la fuerza que nos empuja se hace mayor.
► DEDUCCIÓN DE LAS FORMULAS:
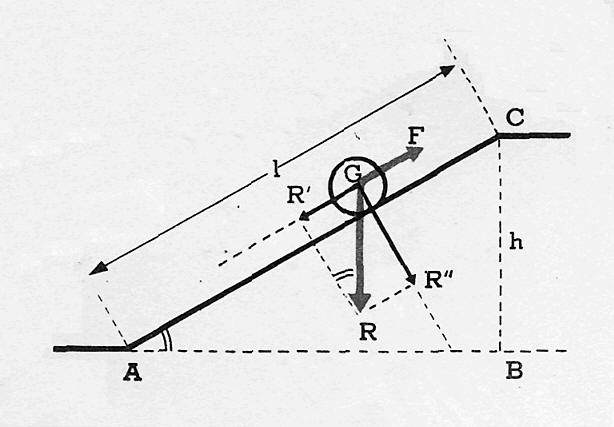
La figura superior muestra un plano inclinado, y un barril cuyo peso es la resistencia R, que se debe equilibrar con la fuerza motriz F. Para hallar la condición de equilibrio, descompongamos la resistencia R en dos: R', paralela al plano inclinado, y R", perpendicular al mismo. Como ésta queda anulada por la reacción del plano, la que hace deslizar al barril hacia abajo es R'.
A ella, pues, se debe anular, y la condición es que sea F igual y opuesta a R'.
Observando la figura se advierte que los triángulos GR´ R" y ABC son semejantes, por ser rectángulos y tener el ángulo A = R (pues sus lados son perpendiculares entre sí y ambos son agudos). Por lo tanto, sus lados homólogos son proporcionales.
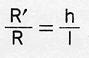
Cuando hay equilibrio se cumple que F=R´ (sino hay equilibrio el cuerpo se movería)
F . l = R. h
La condición de equilibrio en el plano inclinado es que el producto de la fuerza motriz por la longitud del plano sea igual al producto de la resistencia por la altura del mismo.
Ejemplo: Debemos mantener en equilibrio un tambor sobre un plano inclinado de 5 m de longitud y 2 m de altura. ¿Qué fuerza F es necesario aplicar, si el peso del tambor es de 80 Kg.?
En la fórmula anterior: F . l = R . h despejamos F=R. h/l ==> 80 . 2 / 5 = 32 Kg.
Para los que saben trigonometría y observan en factor (h/l), representa al seno del ángulo en A, ósea que sino tenemos el largo o la altura del plano podemos medir el ángulo en A, y buscar el seno.
Ejemplo: Sobre un plano inclinado hay un barril de 1.000 N. Calcular la fuerza necesaria para mantenerlo en equilibrio, sabiendo que el plano forma un ángulo de 30° con la horizontal.
Aplicando la fórmula hallada: F . l = R . h ===> F= R . (h/l) = R. sen(30°)= 1000. 0,50 = 500 N.
• MULTIPLICACIÓN DEL PLANO INCLINADO
De la condición de equilibrio: F=R. (l/h)
El factor (l/h) es la multiplicación del plano. h Por ejemplo, si un plano que llega hasta una altura de 60 cm tiene una longitud de 2,4 m, la multiplicación vale 2,4 m : 0,6 m = 4; se podrá mantener en equilibrio cualquier cuerpo con sólo hacer una fuerza motriz igual a la cuarta parte de su peso.
Ejemplo:
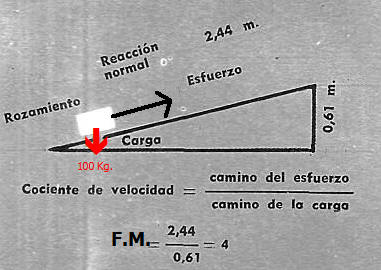
Por lo tonto, si no hubiere resistencia debida a rozamientos, una carga de 100 Kg. se podría subir por el pleno con un esfuerzo de 25 Kg. Pero en la práctica sería de 35 Kg. a 45 Kg., según la naturaleza de las superficies.
------------- 00000 ------------
► CONSIDERACIONES PRÁCTICAS:
Se requiere una fuerza mayor para mover la carga en un plano con fuerte ángulo de inclinación que en otro menos inclinado. Sin embargo, el trabajo total que se requiere para levantar la carga a una misma altura es el mismo, cualquiera que sea el ángulo de inclinación del plano.
Por otra parte, se ha de realizar un trabajo adicional para vencer las fuerzas de fricción entre la carga y el plano, y éstas son menores cuanto mayor sea el ángulo de inclinación del plano con la horizontal.
El cociente de velocidad de cualquier máquina se obtiene dividiendo la distancia a lo largo de la cual se traslada la fuerza aplicada (o esfuerzo) por la altura a la cual se eleva la carga.
Como en las otras máquinas, el cociente de velocidad de un plano inclinado se calcula a partir de sus dimensiones.
La distancia que recorre la fuerza aplicada es la distancia a lo largo del plano, mientras que la distancia a la cual se eleva la carga es la altura a la que se encuentra.
Puesto que las fuerzas de fricción, o rozamiento, tienen un efecto mucho mayor en el rendimiento del plano inclinado que en otras máquinas (especialmente poleas), se gana muy poco intentando calcular la ventaja mecánica (carga/esfuerzo) a partir de consideraciones teóricas.
Es más conveniente encontrar experimentalmente la ventaja mecánica, y utilizarla como un medio de calcular la magnitud de las fuerzas de rozamiento.
La fricción por la acción de rodar que se experimenta al cargar barriles (y otros objetos de sección circular) es pequeña si se compara con la fricción de deslizamiento que se debe vencer cuando se empujan cajas (o se tira de ellas) por un plano inclinado.
Por esta razón, el plano inclinado se ha utilizado durante muchos años para cargar barriles.
Recientemente, sin embargo, el trabajo adicional necesario para cargar cajas se ha reducido considerablemente, mediante el empleo de planos inclinados provistos de rodillos metálicos.
En este caso, los rozamientos se han reducido al cambiar la fricción de deslizamiento por fricción de rodadura.
► ¿Qué es una Máquina?
Esta pregunta fue planteada al empezar la discusión de las máquinas. Ahora ya se debería tener un conocimiento claro de lo que un físico quiere decir con ese término.
Una máquina es un dispositivo mecánico que hace posible obtener trabajo más convenientemente.
La máquina por sí misma no es una fuente de energía; por el contrario, hay que alimentarla y modifica el trabajo en una de las tres maneras siguientes:
1. La dirección de la fuerza puede cambiarse para aplicarla con más comodidad. Con una polea fija, por ejemplo, se puede levantar una carga tirando hacia abajo en lugar de hacia arriba. En este caso, la ventaja mecánica es 1.
2. La magnitud de la fuerza puede variarse de modo que una pequeña fuerza de la potencia se use para vencer una gran fuerza de la resistencia. El plano inclinado se emplea así, en general, lo mismo que la mayoría de los sistemas de poleas, el torno y muchas palancas, como la barreta. En este caso, la ventaja mecánica es mayor que 1.
3. La magnitud de la fuerza puede disminuirse con objeto de que la rapidez o la distancia se aumenten. Esta es la situación en la caña de pescar, la batidora de huevos y la bicicleta. Aquí la ventaja mecánica es menor que 1. La mayoría de las máquinas utilizan el principio del plano inclinado o de la palanca, aunque algunas no pueden analizarse de este modo.
----------- 0000 -----------
• ANEXO:
Concepto de Momento Flector o Cupla,Generos de Palancas y Ejemplos
Para abrir una puerta le "aplicamos" una fuerza y la puerta gira sobre sus bisagras.
El efecto de giro de la fuerza que "aplicamos" es su momento.
El lugar alrededor del cual se produce la rotación, en este caso las bisagras, es el eje.
Si empujamos la puerta apoyándonos en el borde la podremos abrir muy fácilmente; si en cambio empujamos en algún lugar cercano a las bisagras, el esfuerzo tendrá que ser mayor.
Esto se debe a que una fuerza pequeña, actuando a gran distancia del eje, puede tener el mismo momento que una fuerza de gran intensidad que actúe cerca del eje.
Definimos el momento de una fuerza como el producto de la misma por la distancia entre la línea de acción de la fuerza y el eje (Momento = fuerza X distancia).
Las unidades de momento son las correspondientes a longitud y fuerza, ya sea kilogramo-metro o centímetro-gramo, por ejemplo.
Observando las ilustraciones, para el caso de los niños en el "sube y baja" la distancia entre la línea de acción de las fuerzas (los pesos de cada uno) y el eje de rotación es la distancia entre el niño y el eje o apoyo; pero en el caso del pedal de bicicleta, la distancia no es la longitud de la palanca del pedal.
Esto lo decimos para recordar que el concepto físico de momento requiere considerar siempre la distancia a la recta de acción de la fuerza.
Cuando el efecto de giro de una fuerza tiende a mover un objeto en sentido opuesto al de las agujas de un reloj, solemos decir, convencionalmente, que se trata de un momento positivo. El contrario, negativo.
Temas Relacionados:
Concepto Físico de Momento o Cupla - Géneros de Palancas
Demostración Rotación Terrestre Experimento Pendulo de Foucault
Las Leyes del Pendulo Fisico: Oscilacion, Periodo y Aplicaciones
Concepto de Momento Flector o Cupla,Generos de Palancas
Maquinas Simples: Tipos de Palancas, Poleas, Plano Inclinado
Principio de Funcionamiento de Maquina Termicas Calderas
Uso de las Fuerzas Naturales:Aplicaciones del Viento, Calor y Agua
El Conocimiento Científico La Fisica y de la Naturaleza
Descomposición de Fuerzas en un Plano Inclinado
Enlace Externo:• Máquinas simples: historia, características, tipos