Principio de Bernoulli:Teorema de la Hidrodinamica:Teoria Resumida
Principio de Bernoulli - Teorema de la Hidrodinámica
INTRODUCCIÓN GENERAL:
Se denominan fluidos aquellos cuerpos cuyas moléculas tienen entre sí poca o ninguna coherencia y toman la forma de la vasija que los contiene, como los líquidos y los gases.
Muchos de dichos cuerpos fluyen con bastante facilidad y raramente permanecen en reposo.
La rama de la ciencia que trata de los fluidos en movimiento se conoce con el nombre de Hidrodinámica.
Como ejemplo, se puede citar el agua que circula por una tubería, o la corriente de aire que se origina sobre las alas de un avión en vuelo.
El comportamiento de un fluido en movimiento es, naturalmente, más complicado que el de un fluido en reposo.
En Hidrostática (rama que trata de los fluidos en reposo), lo más importante de conocer, acerca del fluido, es la presión que actúa sobre el mismo.
Un buzo experimenta tanto mayor aumento de presión cuanto mayor es la profundidad a la que está sumergido en el agua; la presión que soporta a una determinada profundidad es, simplemente, la suma del peso del agua por encima de él, y la presión del aire sobre la superficie del agua.
Cuando el agua se pone en movimiento, la presión se modifica.
Es casi imposible predecir cuál es la presión y la velocidad del agua, por lo que el estudio de los fluidos en movimiento es muchísimo más complicado que el de los fluidos en reposo.
Un buzo que se mueve a lo largo, y en el mismo sentido que una corriente submarina, probablemente no nota que la presión alrededor de él cambia.
Pero, de hecho, al ponerse el agua en movimiento, la presión disminuye y, cuanto mayor es la velocidad, mayor es la caída de presión.
Esto, en principio, sorprende, pues parece que un movimiento rápido ha de ejercer una presión mayor que un movimiento lento.
El hecho real, totalmente opuesto, fue primeramente expresado por el matemático suizo Daniel Bernoulli (1700-1782).
Si un fluido comienza a moverse, originando una corriente continua, debe existir alguna causa que origine dicho movimiento.
Este algo es una presión.
Una vez el fluido en movimiento, la presión cambia, bien sea aumentando o disminuyendo.
Supongamos que aumenta.
Al aumentar la presión, crece la velocidad del fluido, que origina un nuevo aumento en la presión; este aumento hace crecer el valor de la velocidad, y así sucesivamente.
PRINCIPIO DE LA HIDRODINÁMICA: EXPLICACIÓN RESUMIDA DE LA TEORÍA:
A continuación estudiaremos la circulación de fluidos incompresibles, de manera que podremos explicar fenómenos tan distintos como el vuelo de un avión o la circulación del humo por una chimenea.
El estudio de la dinámica de los fluidos fue bautizada hidrodinámica por el físico suizo Daniel Bernoulli, quien en 1738 encontró la relación fundamental entre la presión, la altura y la velocidad de un fluido ideal.
El teorema de Bernoulli demuestra que estas variables no pueden modificarse independientemente una de la otra, sino que están determinadas por la energía mecánica del sistema.
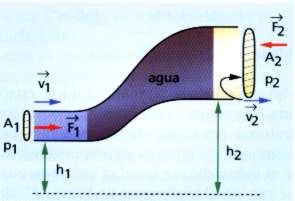 Supongamos que un fluido ideal circula por una cañería como la que muestra la figura.
Supongamos que un fluido ideal circula por una cañería como la que muestra la figura.
Concentremos nuestra atención en una pequeña porción de fluido V (coloreada con celeste): al cabo de cierto intervalo de tiempo Dt (delta t) , el fluido ocupará una nueva posición (coloreada con rojo) dentro de la Al cañería. ¿Cuál es la fuerza “exterior” a la porción V que la impulsa por la cañería?
Sobre el extremo inferior de esa porción, el fluido “que viene de atrás” ejerce una fuerza que, en términos de la presiónp1, puede expresarse como p1 . A1, y está aplicada en el sentido del flujo.
Análogamente, en el extremo superior, el fluido “que está adelante” ejerce una fuerza sobre la porción V que puede expresarse como P2 . A2, y está aplicada en sentido contrario al flujo.
Es decir que el trabajo (T) de las fuerzas no conservativas que están actuando sobre la porción de fluido puede expresarse en la forma:
T=F1 . Dx1- F2. Dx2 = p1. A1. Dx1-p2. A2. Ax2
Si tenemos en cuenta que el fluido es ideal, el volumen que pasa por el punto 1 en un tiempo Dt (delta t) es el mismo que pasa por el punto 2 en el mismo intervalo de tiempo (conservación de caudal). Por lo tanto:
V=A1 . Dx1= A2. Dx2 entonces T= p1 . V - p2. V
El trabajo del fluido sobre esta porción particular se “invierte” en cambiar la velocidad del fluido y en levantar el agua en contra de la fuerza gravitatoria. En otras palabras, el trabajo de las fuerzas no conservativas que actúan sobre la porción del fluido es igual a la variación de su energía mecánica Tenemos entonces que:
T = DEcinética + AEpotencial = (Ec2 — Ec1) + (Ep2 — Ep1)
p1 . V — P2 . V = (1/2 .m . V2² — 1/2 . m. V1²) + (m . g . h2 — m . g . h1)
Considerando que la densidad del fluido está dada por d=m/V podemos acomodar la expresión anterior para demostrar que:
P1 + 1/2 . d. V1² + d . g. h1= P2 + 1/2 . d. V2² + d . g . h2
Noten que, como los puntos 1 y 2 son puntos cualesquiera dentro de la tubería, Bernoulli pudo demostrar que la presión, la velocidad y la altura de un fluido que circula varian siempre manteniendo una cierta cantidad constante, dada por:
p + 1/2. d . V² + d. g. h = constante
Veremos la cantidad de aplicaciones que pueden explicarse gracias a este teorema.
![]()
Analogía con el Fluido Humano.
Una multitud de espectadores pretende salir de una gran sala de proyecciones al término de la función de cine.
El salón es muy ancho, pero tiene abierta al fondo sólo una pequeña puerta que franquea el paso a una galería estrecha que conduce hasta la calle.
La gente, impaciente dentro de la sala, se agIomera contra la puerta, abriéndose paso a empujones y codazos.
La velocidad con que avanza este “fluido humano” antes de cruzar la puerta es pequeña y la presión es grande.
Cuando las personas acceden a la galería, el tránsito se hace más rápido y la presión se alivia. Si bien este fluido no es ideal, puesto que es compresible y viscoso (incluso podría ser turbulento), constituye un buen modelo de circulación dentro de un tubo que se estrecha.
Observamos que en la zona angosta la velocidad de la corriente es mayor y la presión es menor.
![]()
• APLICACIONES PRÁCTICAS:
EL TEOREMA DE TORRICELLI
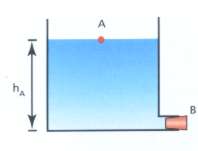 Consideremos un depósito ancho con un tubo de desagote angosto como el de la figura.
Consideremos un depósito ancho con un tubo de desagote angosto como el de la figura.
Si destapamos el caño, el agua circula. ¿Con qué velocidad? ¿Cuál será el caudal?.
En A y en B la presión es la atmosférica PA=PB=Patm.
Como el diámetro del depósito es muy grande respecto del diámetro del caño, la velocidad con que desciende la superficie libre del agua del depósito es muy lenta comparada con la velocidad de salida, por lo tanto podemos considerarla igual a cero, VA = 0
La ecuación de Bernoulli queda entonces:
d. g. hA + pA= 1/2 . d. hB + pB
entonces es:
g . hA = 1/2 . vB² + g. hB de donde VB²= 2. .g . (hA-hB)
de donde se deduce que:
VB² = 2. g(hA - hB)
Este resultado que se puede deducir de la ecuación de Bernoulli, se conoce como el teorema de Torricelli, quien lo enunció casi un siglo antes de que Bernoulli realizara sus estudios hidrodinámicos.
La velocidad con que sale el agua por el desagote es la misma que hubiera adquirido en caída libre desde una altura hA, lo que no debería sorprendernos, ya que ejemplifica la transformación de la energía potencial del líquido en energía cinética.
EL GOL OLÍMPICO
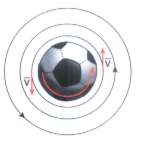
A: Una pelota que rota sobre si misma arrastra consigo una fina capa de aire por efecto del rozamiento.
B: Cuando una pelota se traslada, el flujo de aire es en sentido contrario al movimiento de la pelota.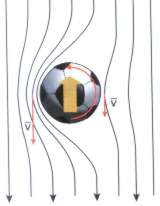
C: Si la pelota, a la vez que avanza en el sentido del lanzamiento, gira sobre sí misma, se superponen los mapas de las situaciones A y B.
El mapa de líneas de corrientes resulta de sumar en cada punto los vectores VA y VB. En consecuencia, a un lado de la pelota, los módulos de las velocidades se suman y, al otro, se restan. La velocidad del aire respecto de la pelota es mayor de un lado que del otro.
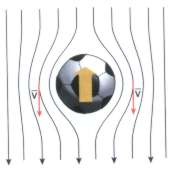
D: En la región de mayor velocidad, la presión (de acuerdo con el teorema de Bernoulli) resulta menor que la que hay en la región de menor velocidad. Por consiguiente, aparece una fuerza de una zona hacia la otra, que desvía la pelota de su trayectoria. Éste es el secreto del gol olímpico.

EL AERÓGRAFO
 Las pistolas pulverizadoras de pintura funcionan con aire comprimido.
Las pistolas pulverizadoras de pintura funcionan con aire comprimido.
Se dispara aire a gran velocidad por un tubo fino, justo por encima de otro tubito sumergido en un depósito de pintura.
De acuerdo con el teorema de Bernoulli, se crea una zona de baja presión sobre el tubo de suministro de pintura y, en consecuencia, sube un chorro que se fragmenta en pequeñas gotas en forma de fina niebla.
FUERZA DE SUSTENTACIÓN:
Cualquier cuerpo que se mueve a través del aire experimenta una fuerza que proviene de la resistencia del aire.
Ésta puede dividirse en dos componentes que forman entre sí un ángulo recto. A uno se lo llama sustentación y se dirige verticalmente hacia arriba.
El otro, llamado resistencia, actúa horizontalmente y en sentido opuesto a la dirección de desplazamiento del cuerpo.
La fuerza de sustentación se opone al peso y la resistencia se opone al movimiento del cuerpo. Para que un cuerpo pueda volar la fuerza de sustentación debe superar al peso y la resistencia debe ser tan reducida que no impida el movimiento.
Para obtener un resultado óptimo necesitamos un cuerpo con una alta relación entre la fuerza de sustentación y la resistencia.
El índice más elevado se obtiene mediante un cuerpo diseñado especialmente que se denomina "perfil aerodinámico".
Por razones prácticas no es posible obtener un perfil aerodinámico perfecto en un aeroplano pero las alas se diseñan siempre de modo que suministren la sustentación que sostiene a la máquina en el aire.
En un corte transversal un perfil aerodinámico exhibe una nariz redondeada, una superficie superior fuertemente curvada, la inferior más achatada y una cola aguzada.
El perfil se inclina formando un ligero ángulo con la dirección del flujo de aire.
La fuerza ascendente se obtiene de dos modos: por encima del perfil aerodinámico el aire se mueve más rápido a causa de su forma curva.
Por el principio descubierto por Bernoulli y resumido en una ecuación matemática, la presión de un fluido disminuye en relación con el aumento de su velocidad y viceversa.
De ese modo, la presión del aire que se mueve en la parte superior del perfil decrece creando una especie de succión que provoca el ascenso del perfil aerodinámico.
Por otra parte el aire que fluye bajo el perfil angulado aminora su velocidad de manera que la presión aumenta.
Esta acción eleva el perfil aerodinámico, dándole mayor poder de sustentación.
La fuerza de sustentación total depende del tipo de perfil, de la superficie de las alas, de la velocidad del flujo y de la densidad del aire.
La fuerza ascensional disminuye con la altitud, donde el aire es menos denso, y aumenta con el cuadrado de la velocidad del aeroplano y también con la mayor superficie de las alas.
El ángulo que forma el perfil aerodinámico con el flujo de aire se llama ángulo de incidencia.
A mayor ángulo, mayor fuerza ascensorial hasta llegar a un punto crítico, después del cual la fuerza ascensorial diminuye bruscamente.
El flujo de aire que hasta el momento había sido suave, se descompone repentinamente en forma de remolinos.
Cuando ello ocurre se dice que el avión se ha desacelerado, y de ser así el avión comienza a caer, pues las alas ya no lo pueden sostener. Es muy peligroso en caso que al avión se encuentre cerca de la tierra.
Flujo de Aire en el Ala de un Avión
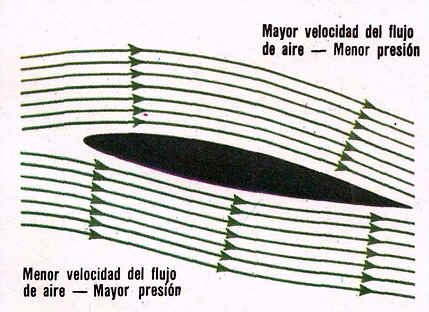
El diagrama muestra una sección en corte del ala de un aeroplano, según un diseño aerodinámico. El aire fluye por encima y por debajo del ala, pero fluye más rápido por encima de la parte superior porque está más curvada, presentando un largo mayor.
El flujo de aire más rápido ejerce menos presión; además, se produce otra presión hacia arriba, resultante de la menor velocidad del aire por debajo del ala, que la proveerá de fuerza ascensional. Ésta es la base del vuelo del aeroplano.
Fuente Consultada: Enciclopedia NATURCIENCIA Tomo 1
Temas Relacionados:
Teorema Fundamental de la Hidrostática
Teorema del Principio de Pascal
Concepto de Momento Flector o Cupla,Generos de Palancas
Maquinas Simples: Tipos de Palancas, Poleas, Plano Inclinado
Principio de Funcionamiento de Maquina Termicas
Ejercicios Elementales de Ciencia, Con Problemas Para Razonar
Uso de las Fuerzas Naturales:Aplicaciones del Viento, Calor y Agua
Tres Principios Basicos de la Física:Pascal Arquimides y Bernoullie
Leyes de la Mecanica Clasica: Principios de Inercia y Masa -Ley
Enlace Externo: Principio de Bernouille





