El Circulo Trigonometrico:Las Funciones Trigonometricas-Explicacion Sencilla
Círculo Trigonométrico - Funciones Seno, Coseno y Tangente
►¿Que es el Círculo Trigonométrico?
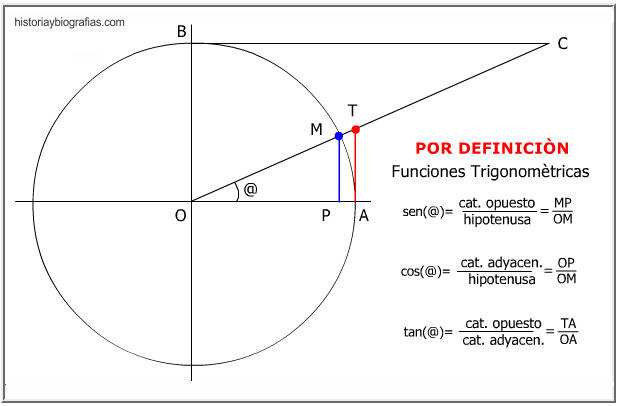
Consideramos la figura de arriba, que se conoce como círculo trigonométrico, y es una circulo de radio=1, donde se definen las funciones trigonométricas.
Las funciones trigonométricas directas definidas en dicho círculo se llaman: seno, coseno, tangente, y las inversas son cosecante, secante y cotangente respectivamente.
• Definición de las Funciones
FUNCIÓN SENO:
Por definición en todo triángulo rectángulo (tiene un ángulo recto=90°) el SENO de un ángulo es igual al cateto opuesto dividido por la hipotenusa de dicho triángulo.
Para el caso de la figura superior, se puede decir que el seno del ángulo @ es la ordenada del extremo del arco cuando el radio es la unidad. O sea, en la figura, corresponde al segmento MP. Por lo tanto el seno de @ será el cociente entre MP y la hipotenusa OM. Definición: sen(@)=MP/OM
FUNCIÓN COSENO:
Por definición en todo triángulo rectángulo (tiene un ángulo recto=90°) el COSENO de un ángulo @ es igual al cateto adyacente dividido por la hipotenusa de dicho triángulo.
► Imagen del Círculo Trigonométrico
En la figura el coseno es la abscisa del extremo del arco, cuando el radio es la unidad; o sea, el segmento OP. Por lo tanto el coseno de @ será el cociente entre OP y la hipotenusa OM. Definición: cos(@)=OP/OM
FUNCIÓN TANGENTE:
Por definición en todo triángulo rectángulo (tiene un ángulo recto=90°) la TANGENTE de un ángulo es igual al cateto opuesto dividido por el cateto adyacente de dicho triángulo.
En la figura la tangente es el segmento de tangente geométrica comprendido entre el origen del arco y la prolongación del radio que pasa por el extremo del mismo; o sea, el segmento AT. Por lo tanto la tangente de @ será el cociente entre el cateto opuesto TA y el cateto adyacente OA. Definición: tan(@)=TA/OA
Ya están representadas todas las funciones trigonométricas directas. Como decíamos antes ahora faltan las inversas, a saber:
Inversa de seno=cosecante=1/sen(@)
Inversa del coseno=secante=1/cos(@)
Inversa de tangente=cotangente=1/tan(@)
► Ejemplo Práctico:
En el triángulo de abajo hallar el seno, coseno y tangente de los ángulos A y C
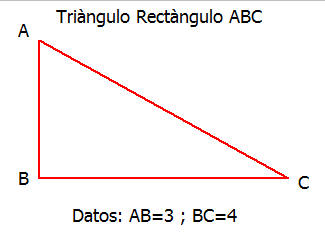
Explicación: Para pode aplicar las formulas definidas vemos que necesitamos el valor de la hipotenusa AC, la cual la podemos obtener por el teorema de Pitágoras, entonces es:
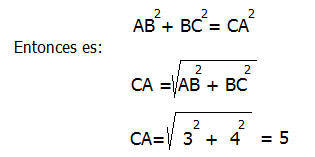
Entonces ahora aplicando las definiciones de arriba es:
Para el ángulo en vértice A es:
sen(A) = BC/CA=4/5=0.80 ----------------- la inversa es cosecante=1/0.80=1.25
cos(A) = AB/CA=3/5=0.60 ----------------- la inversa es secante=1/0.60=1.67
tan(A) = BC/BA=4/3=1.33 ----------------- la inversa es cotangente=1/1.33=0.75
Para el ángulo en vértice C es:
sen(C) = AB/CA=3/5=0.60
cos(C) = BC/CA=4/5=0.80
tan(C) = AB/BC=3/4=0.75
Usando los valores de seno, coseno o tangente del ángulo A, podemos hallar el valor de ese ángulo, con la función arco seno, arco coseno o arco tangente de una calculadora y nos indica que el ángulo vale: A=53° 8´
Usando los valores de seno, coseno o tangente del ángulo B, podemos hallar el valor de ese ángulo, con la función arco seno, arco coseno o arco tangente de una calculadora y nos indica que el ángulo vale: B=36°52´
Obsérvese que si sumamos los ángulos A+B+90°=180°, que justamente es el valor de la suma de los ángulos interiores de un triángulo.
También nos permite deducir que si conocemos un solo ángulo de un triángulo rectángulo podemos obtener por diferencia el otro, sin recurrir a ninguna función trigonométrica.
Hacer Prácticas Online Para Afianzar lo Aprendido
GRAFICA DE LAS FUNCIONES TRIGONOMÉTRICAS:SENO, COSENO Y TANGENTE
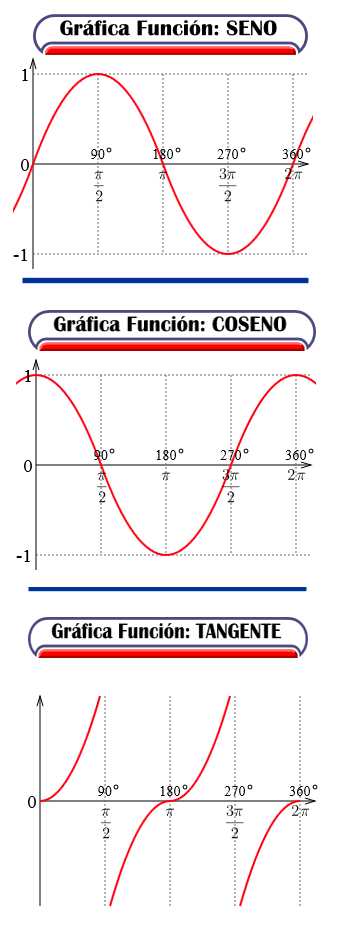
AMPLIACIÓN: Es evidente que las relaciones que existen entre ellas han de ser numerosas, porque, en realidad, por cada teorema de geometría plana que se pueda aplicar a esta figura se obtendrá, por lo menos, una relación.
Vamos a demostrar las más conocidas.
Por ejemplo, si aplicamos el Teorema de Pitágoras al triángulo MPO (la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa), tendremos:
![]()
Pero: MP = Sen @ ; OP = Cos @ y OM = 1 (el radio es la unidad); luego, sustituyendo:
![]()
que es una relación muy importante en trigonometría.
Si consideramos ahora los triángulos semejantes OMP y OTA, se podrá escribir:
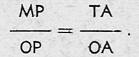
Pero: MP = Sen @ ; OP = Cos @ ; TA = tag @ , y OA = 1 (es el radio).
Luego, sustituyendo:
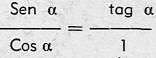
O lo que es igual escribir:
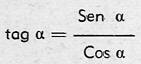
Que es otra relación trigonométrica importante.
Análogamente al caso anterior, de la semejanza de los triángulos OMP y COB, se puede escribir:
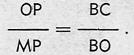
Pero: OP = Cos @ ; MP = Sen a@; BC = Cot @ y BO = 1. Luego, sustituyendo:
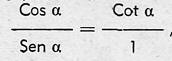

Las tres relaciones deducidas de forma puramente geométrica tienen gran importancia y, combinándolas entre sí, permiten deducir otras muy interesantes también.
Temas Relacionados:
Resolvente de Segundo Grado Online Resolucion Ecuacion
Aplicar la Resolvente Para Ecuaciones de Segundo Grado
Propiedades de las Raices de una Ecuación Cuadratica
Formula del Vértice de una Parabola Cuadrática
Sistema de Ecuaciones Lineales:Resolucion Online
Tartaglia Nicolás:Matemático y su Metodo de Resolver Una Ecuación
Enlace Externo:• Las Funciones trigonométricas