Historia del Descubrimiento de la Fuerza de Gravedad Por Newton
Historia del Descubrimiento de la Fuerza de Gravedad Por Newton, Obra Cientifica -
El rol de las manzanas en la elaboración de la Teoría de La gravedad de Newton puede ser tan anecdótico como la manzana que originó la expulsión de Eva del Paraíso, la manzana de París que desencadenó la Guerra de Troya o la manzana de Guillermo Tell.
Uno de los mayores avances de la historia de la ciencia fue la comprensión por Isaac Newton de que las leyes de la gravedad son aplicables a la Luna y otros cuerpos celestes igual que a los objetos cercanos a la superficie terrestre.
Animado por Edmond Halley y Robert Hooke, finalmente creó las fórmulas matemáticas y las consignó en sus Principia, el libro científico más importante publicado jamás.
Newton reflexionó mucho y llegó a concebir ideas, que cambiaron completamente el concepto humano acerca del Universo. He aquí su modo de razonar:
"La manzana cae por la atracción de la Tierra", (esta no era una idea nueva). Quizás la manzana también atrae a la Tierra, (esta sí era una idea nueva). Puede ser que las manzanas se atraen entre sí.
Es posible que todos los cuerpos se atraen entre sí, (aquí estaba llegando Newton más lejos que las ideas científicas de entonces, dando de inmediato el gran paso).
Tal vez la fuerza de atracción gravitacional entre varios objetos actúa incluso a muy grandes distancias; así, la Tierra y la Luna se atraen mutuamente, igual que el Sol y los planetas y, posiblemente, que el Sol y las estrellas.
------------- 00000 ------------
Al parecer, Newton tuvo los primeros atisbos de una idea sobre la gravitación universal en 1665-1666, su época creativa más fructífera.
Muchos años después afirmó que el concepto de gravedad aplicable por igual a los objetos que se encuentran sobre la Tierra y a las estrellas y planetas le fue inspirado por la visión de una manzana que caía de un árbol.
Según William Stukeley, biógrafo de Newton, estaban almorzando juntos en Kensington el 15 de abril de 1726 y «el día era caluroso, salimos al jardín y bebimos té a la sombra de unos manzanos, a solas.
En medio de aquella conversación, me confesó que estaba justamente en la misma situación cuando tiempo atrás le vino a la mente la idea de la gravitación».
Newton le refirió que vio caer una manzana y se preguntó: «¿Por qué la manzana cae siempre perpendicular al suelo?.
¿Por qué no lo hace de lado, o hacia arriba?.
Sin duda, la razón es que la tierra la atrae; debe existir un poder de atracción en la materia, y la suma del poder de atracción en la materia de la tierra debe estar en su centro».
Newton se preguntó acerca de la extensión de la atracción de la gravedad; evidentemente, llegaba desde el centro de la Tierra hasta la copa del manzano, pero ¿podría llegar hasta la Luna?.
Si así fuera, seguramente afectaría a su órbita. De hecho, ¿podría controlar la órbita de la Luna?.
Hizo algunos cálculos y «parecían responder bastante aproximadamente».
Esta teoría destronó la noción aristotélica de que los cuerpos celestes eran muy diferentes de la Tierra y sin conexión con ella. También negaba las teorías del filósofo y matemático Rene Descartes, según las cuales estrellas y planetas giraban en vórtices.
Fue una idea revolucionaria, pero el hecho de que, se le ocurriera en 1665-1666 en un destello de genialidad es discutible; al parecer no mencionó el episodio de la manzana hasta 1726, sesenta años después de suceso.
La teoría pudo ser resultado de años de trabajo, y probablemente debía tanto a su síntesis de la obra de otros grandes científicos -Copérnico, Kepler, Galileo y Hooke- como a su propio genio natural.
La vinculación entre la fuerza que mantiene a la Luna orbitando alrededor de la Tierra y la que provoca la caída de los cuerpos librados a su propio peso, es en cambio mucho menos anecdótica y forma parte de la obra de Newton (1642-1727), publicada en los Principia (Philosophiae Naturalis Principia Matematica) de 1687, quien le dio sustento matemático y físico, basándose en el andamiaje experimental proporcionado por Kepler y en el esquema de pensamiento elaborado por Galileo.
Hoy, las mismas ideas que explican la caída de las manzanas y el movimiento orbital de los planetas, este enorme edificio intelectual cuya construcción comenzó hace más de 400 años, son utilizadas por los modernos vehículos espaciales para recorrer el espacio interplanetario y han permitido que un producto humano, el Voyager 2, se encuentre ya fuera de los confines de nuestro sistema planetario, vagando por el medio interestelar.
Uno de los problemas que presentaba el movimiento de la Tierra para el sentido común era por qué los cuerpos tirados hacia arriba caen esencialmente sobre el lugar desde el que fueron arrojados si durante su trayectoria en el aire no deberían seguir el movimiento de la Tierra.
Galileo introdujo el concepto de inercia, que permite resolver esta aparente paradoja.
La inercia es la tendencia que posee todo cuerpo en movimiento a continuar en movimiento (como el caso de un jinete cuyo caballo se detiene súbitamente).
Una piedra arrojada desde el mástil de un barco en movimiento cae al pie del mismo y no detrás, ya que comparte el movimiento del barco.
Es sencillo entender con este principio por qué los pájaros, las nubes y la atmósfera en general no quedan detrás de la Tierra en movimiento.
La experiencia nos muestra que los objetos están inmóviles a menos que alguna fuerza actúe sobre ellos.
Cualquier objeto abandonado a sí mismo, si no se mueve permanecerá quieto y si se está moviendo llegará finalmente a su estado "natural” de reposo: una pelota picando alcanzará cada vez una altura menor hasta que finalmente terminará por detenerse; si la pelota está rodando se detendrá al cabo de un tiempo, a no ser que alguien la empuje o que se mueva sobre un plano inclinado.
La Luna y los planetas, en cambio, han permanecido en movimiento a través de los siglos y éste parece ser su estado “natural”; es necesario entonces encontrar cuál es la fuerza que les impide quedarse quietos o qué los hace diferentes de los objetos que existen sobre la Tierra.
La aparente contradicción entre los estados “natural” de los distintos cuerpos fue atacada científicamente por primera w por Galileo y Newton.
La clave de su resolución está en distinguir distintos tipos de movimiento y en reconocer que no hay nada de particular e el estado de reposo.
Newton enunció las leyes que permiten describir el movimiento de los cuerpos.
La primera ley establece que un cuerpo en repos. o que se mueve en línea recta a velocidad constante permanecerá en reposo o en movimiento uniforme a menos que sobre ellos actúe una fuerza ex terna.
¿Cómo explicar entonces que la pelota se detenga?
Para frenar o acelerar un cuerpo, es decir para apartarlo de su movimiento rectilíneo uniforme es necesario aplicar una fuerza.
En el caso de la pelota, esta fuerza se llama fricción o rozamiento y es un proceso muy complicado que todos hemos usado alguna vez, por ejemplo para frenar la bicicleta apoyando unen el suelo.
Isaac Newton comprendió que no había nada que explicar respecto de la velocidad uniforme, lo que requiere explicación son los cambios de velocidad, o más precisamente de momento, siendo éste proporcional a la velocidad (la constante de proporcionalidad es la masa del cuerpo); es decir, cómo cambia la velocidad en presencia de una fuerza. Estos cambios de velocidad, llamados aceleración, ocurren no sólo si la velocidad aumenta o disminuye, sino también si se modifica la dirección del movimiento.
Si viajáramos dentro de una caja cerrada con movimiento rectilíneo uniforme, según el principio de relatividad de Newton, no nos daríamos cuenta de que nos movemos, necesitaríamos alguna referencia externa.
Si la caja se detiene, en cambio, o si se modifica su velocidad, reconoceríamos este cambio de movimiento
Una manera de medir la aceleración es utilizar flechas para representar la velocidad de un cuerpo: la dirección de la flecha indica el sentido del movimiento y su longitud, la magnitud de la velocidad.
Comparando las flechas de velocidad en dos instantes distintos, la diferencia entre ambas representa la aceleración.
Cuando un automóvil que viaja en línea recta aumenta (o disminuye) su velocidad, la aceleración (o desaceleración) está en la misma dirección del movimiento.
Pero cuando el auto dobla en una curva, aunque mantenga su velocidad constante, la diferencia de direcciones de las flechas de velocidad en dos posiciones distintas sobre la curva indicará una aceleración no nula.
Esto es exactamente lo que sucede en el movimiento planetario: la flecha de aceleración de los planetas apunta siempre hacia el Sol.
Allí está la causa del movimiento: los planetas están “cayendo” permanentemente hacia el Sol, de la misma manera en que los objetos caen hacia la Tierra si son abandonados a su propio peso: la flecha de aceleración de una manzana madura que ya no es sostenida por la rama del árbol apunta hacia el centro de la Tierra.
Esta idea de la caída de los planetas hacia el Sol o de la Luna hacia la Tierra, no parece muy adecuada ya que no vemos caer a estos cuerpos.
Sin embargo hay que pensar que si los planetas no estuvieran cayendo se alejarían cada vez más del Sol, siguiendo una trayectoria rectilínea.
En realidad fue Borelli (1608-1679), contemporáneo de Newton, quien observó que un cuerpo en movimiento circular mostraba una tendencia a alejarse del centro, la que, en el caso de los planetas, debía suponerse balanceada por algún tipo de atracción hacia el Sol.
Aparece así por primera vez la idea de que el movimiento de los planetas debía explicarse no por una fuerza actuante en la dirección en que se mueven, sino por una fuerza dirigida hacia el Sol, es decir perpendicular a la dirección del movimiento.
Independientemente del aspecto planetario este problema podría reducirse a estudiar bajo qué condiciones un cuerpo puede girar con velocidad circular uniforme.
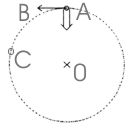Supongamos que el punto A de la figura representa la posición de un cuerpo con movimiento uniforme en un círculo centrado en 0.
En este instante el cuerpo se está moviendo en dirección tangente al círculo (su velocidad se indica con la flecha AB).
En consecuencia, de acuerdo a la primera ley de Newton, si se abandona el cuerpo a sí mismo, en ausencia de todo otro cuerpo, seguirá moviéndose en la misma dirección (es decir, a lo largo de AB) y un momento más tarde se encontrará en B.
Pero en realidad se encuentra en c, sobre el círculo. Por lo tanto debe haber habido alguna influencia que hizo “caer” el cuerpo de B a C, acercándolo al centro 0.
La curvatura de las órbitas de los planetas y los satélites mide el apartamiento respecto de la trayectoria rectilínea que seguirían si no hubiera otros cuerpos que causaran la desviación.
Galileo dedujo la relación (las leyes) entre las distancias recorridas por los cuerpos y los tiempos empleados en recorrerlas, para distintos tipos de movimientos (rectilíneo uniforme, uniformemente acelerado, curvilíneo).
Construyó así la tabla de datos que, junto a las leyes de Kepler, permitieron a Newton encontrar el principio físico y matemático sobre el que se sustentan.
Para imprimir a un cuerpo una aceleración se necesita una fuerza proporcional a ella.
El factor de proporcionalidad, de acuerdo a la segunda ley de Newton, es la masa del cuerpo: necesitamos realizar el doble de esfuerzo para mover un cuerpo cuya masa es el doble de la de otro.
Partiendo del descubrimiento de Galileo de que todos los cuerpos caen con igual aceleración, independientemente de sus masas (el Supuesto experimento realizado en la Torre de Pisa), se puede concluir, usando la segunda ley de Newton que las fuerzas que los atraen son proporcionales a Sus masas.
Es la fuerza de gravedad que actúa sobre los cuerpos en caída libre y la aceleración provocada por ella es la aceleración de la gravedad: g=GM/R2.
G es una constante conocida como la constante de gravitación universal o constante de Newton, M se refiere a la masa del cuerpo que provoca la aceleración y R es la distancia entre éste y el cuerpo atraído.
La tercera ley de Newton se expresa entonces matemáticamente como
F=(GmM)/R2 (1)
Así, la fuerza ejercida por la Tierra (de masa M) sobre la Luna (cuya masa representamos por m) será mucho mayor que la ejercida por la Tierra sobre una manzana (de masa mucho menor que la de la Luna), y la atracción gravitatoria entre dos manzanas será perfectamente despreciable.
Utilizando los datos de que disponía sobre la Luna, su distancia a la Tierra y su período de traslación Newton advirtió que la fuerza de atracción entre dos cuerpos satisface una ley de cuadrado inverso, es decir, disminuye como el cuadrado de la distancia que los separa, como indica la fórmula (1).
Esta ecuación resume el contenido de su tercera ley o ley de gravitación universal.
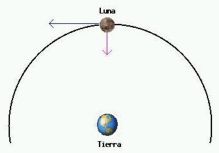
Newton obtuvo así que la fuerza de gravedad en la Luna era menor que sobre la Tierra (un objeto de 70 Kg. sobre la Tierra pesaría 10 Kg. en la Luna).
Las diferencias entre la aceleración gravitatoria en las superficies de los planetas y en sus satélites (consecuencia de sus distintos tamaños y masas) han dado lugar a una prolífica literatura de ciencia ficción.
Se ha propuesto por ejemplo un ingenioso juego de baseball en Deimos (satélite de Marte) donde la velocidad impresa a una pelota por un bateador profesional sería suficiente para lanzarla en órbita alrededor del satélite.
El bateador podría retirarse a tomar unos mates (si fuera argentino) y volver a las 2 horas, cuando la pelota ha regresado de su órbita para lanzarla nuevamente en sentido opuesto o simplemente recuperarla.
Más allá de la diversión, la fuerza gravitatoria de un planeta es una medida de su capacidad, por ejemplo, para retener una atmósfera.
Si la fuerza de gravedad en la Tierra hubiera sido distinta, las formas de vida que se han desarrollado sobre nuestro planeta también hubieran diferido en su evolución y aspecto.
En las actuales condiciones, las aves vuelan porque mantienen el mismo peso posible: sus huesos son huecos y sus cerebros de capacidad ínfima.
Si la gravedad fuera menor estarían seguramente mejor equipadas y ocuparían tal vez un puesto más alto en la jerarquía de las especies.
La manzana y la luna from alexiscb on Vimeo.
------------- 00000 ------------
La fuerza del niño es menor que la del adulto y la atracción de la Tierra o gravedad, que resta igual impulso a ambos proyectiles, hace que el primero alcance menor altura y caiga antes hacia la Tierra.
Existe una velocidad, llamada velocidad "de escape", muy difícil de calcular porque depende de muchos factores, que permite a un proyectil lanzado verticalmente escapar definitivamente a la decreciente atracción terrestre.
Según la ley de inercia, los proyectiles lanzados por el hombre y el niño proseguirían en línea recta y con velocidad uniforme.
Pero la fuerza de gravedad hace que simultáneamente vayan cayendo hacia el mar, según curvas que dependen de su velocidad inicial.
Las estrellas, que forman las nebulosas o galaxias, que son como las islas del universo, no se apartan unas de otras debido a la fuerza de la gravitación, pero tampoco se concentran en una sola masa debido a la fuerza centrífuga de sus enormes velocidades individuales, que tienden a hacerlas evadir en línea recta. La galaxia gira como un sistema solar
El radio de la Luna es sólo un cuarto del de la Tierra; su densidad relativa, 0,6 de la de ésta. Multiplicando ambas cantidades deducimos que la atracción de la Luna alcanza únicamente a la sexta parte de la gravedad de la Tierra.
Un atleta que puede saltar a sólo 2 m. de altura en la Tierra, llegará a 12 m. en la Luna. Por otra parte, el peso de su cuerpo será seis veces menor, y el esfuerzo de su corazón para que su sangre vuelva desde los pies hasta la aurícula derecha, o para irrigar su cerebro, será también menor.
------------- 00000 ------------
Una vez enunciados estos principios, Newton debía demostrar que de ser exactos, las órbitas de los planetas obedecerían las leyes experimentales de Kepler.
Resolviendo las ecuaciones diferenciales que se obtienen aplicando las fórmulas newtonianas al movimiento planetario es posible deducir, con bastante exactitud, las 3 leyes keplerianas.
Para elaborar su teoría Newton necesitó desarrollar la matemática del cálculo diferencial de la cual no disponía y esto fue lo que demoró la publicación de su obra.
Esta es una situación que se encuentra a menudo en física: al no contar con las herramientas matemáticas necesarias para afrontar un problema físico, muchas veces esta disciplina motivó el desarrollo de partes de las matemáticas que posteriormente encuentran aplicación en otras áreas.
Aunque las órbitas planetarias están relativamente bien descriptas por las leyes de Kepler, de acuerdo con la ley de gravitación universal habrá perturbaciones producidas por la presencia de otros planetas en el sistema solar y de los satélites naturales.
Estas perturbaciones, proporcionales al cuadrado de sus distancias mutuas hacen que el camino de los planetas oscile alrededor de una elipse media.
Si los planetas fueran mucho más masivos o si estuvieran mucho más próximos entre sí, su movimiento no podría ser descripto, ni siquiera en una primera aproximación por las leyes de Kepler (obtenidas de la llamada aproximación de dos cuerpos, que en este caso son el Sol y el planeta).
Habría que resolver el denominado problema de N cuerpos, donde N se refiere al Sol, el planeta y los otros cuerpos que perturban.
Los movimientos resultantes serían muy complejos.
La aplicación de la ley de la gravitación universal de Newton permitió descubrir dos planetas, Neptuno y Plutón, demostrando así su capacidad, no sólo de explicar los fenómenos observados sino también su enorme poder predictivo.
El descubrimiento de un cuerpo celeste, a 4 mil millones de kilómetros de la Tierra, mediante un simple cálculo matemático, representa un hito fundamental en la historia de la ciencia.
Desde fines del siglo XVIII los astrónomos tenían problemas en conciliar sus cálculos con las posiciones observadas de Urano.
Aplicando la tercera ley de Newton a un supuesto cuerpo perturbador de la órbita fue posible calcular la masa y la Posición de este hipotético objeto con suficiente precisión como para descubrir Neptuno.
Los cálculos teóricos fueron publicados por U. J. Leverrier (1811-1877) en junio de 1846 y el nuevo planeta fue observado efectivamente el 23 de septiembre siguiente en el Observatorio de Berlín.
El entusiasmo provocado por este descubrimiento motivó la búsqueda de un posible noveno planeta.
Los datos sobre la órbita de Neptuno no eran todavía muy precisos, lo que demoró 25 años la primera observación de Plutón, desde que fuera predicho en 1905.
Estos descubrimientos también muestran que la fuerza de la gravedad actúa a gran escala, al menos su influencia llega hasta los confines más exteriores del sistema solar.
El radio de la Tierra es tan enorme que a 8 Km. de altura el peso de un objeto disminuye en sólo algo más de 2 gr. por kilogramo (puesto que la distancia aumentó en una milésima de radio, y debe elevarse al cuadrado, es decir multiplicarse por sí misma).
A 15 Km. de altura un kilogramo pierde entre 4 y 5 gr. de peso. A 100 Km. la reducción es de unos 22 gr. por Kg.; a los 1.000 Km. pasa de los 200 gr. por kilo y a los 4.500 Km. el peso decrece a la mitad. Cuanto más nos alejamos tanto menor se vuelve fa atracción.
APLICACIONES Y CONSECUENCIAS
• La gravimetría es el método de elección, entre muchos, para revelar la existencia de petróleo: éste, tres o cuatro veces más liviano que las tierras que impregna, asciende hasta colocarse sobre las cúpulas de roca densa e impermeable.
El gravímetro, que consiste en esencia en un peso que tira un resorte, es capaz de señalar esas diferencias locales de densidad de masa, es decir de atracción.
Se lo usa en menor escala para descubrir yacimientos de hierro, sumamente densos.
• A la gravitación se deben las mareas, las órbitas de los planetas (la atracción del Sol equilibra su tendencia a escapar en línea recta), la presencia de atmósfera en la Tierra (la Luna, de atracción muy débil, perdió la suya), y la caída de la lluvia cuando las gotas alcanzan a 1/20 de mm. de diámetro (cuando son menores, las corrientes ascendentes equilibran su peso).
La dificultad de un vehículo espacial para escapar de la atracción terrestre se debe en primer lugar a la fricción de la atmósfera, que es ya casi nula a los 100 Km. de altura; y en segundo lugar a la gravedad terrestre, que disminuye muy lentamente.
• Se llama relación de masa en un cohete espacial a la proporción entre la masa del proyectil a la salida y el peso útil puesto en órbita. Si dicho cociente es mayor de 8, no queda margen práctico para colocar instrumentos. De allí que los cohetes tengan varias etapas.
• Se ignora por completo la naturaleza de la gravitación y se estima que se necesitarán unos 100 años para dilucidarla y "desviarla" de alguna manera.
• Los animales sometidos a una "gravedad" elevada (centrifugadora) crecen enanos; en los astronautas sin peso el calcio tiende a emigrar de los huesos a los riñones.
• Los viajeros de un avión pesan pues éste es como una plataforma sostenida por las alas.
• Para breves ensayos de falta de gravedad existe un avión especial, el C-131, que "cae" como un ascensor que bajara velozmente.
Fuente Consultada: Notas Celestes de Carmen Núñez
Ver: Conflicto Newton - Hooke Por Las Órbitas de los Planetas
