Origen de la Geometría:Historia,Matematicos y un Curso Basico
Origen de la Geometría-Historia y Sus Matematicos - Curso Basico
GEOMETRÍA. Parte de las matemáticas que trata de las propiedades y medida de la extensión.
En su origen, la geometría tuvo una finalidad eminentemente práctica, como lo revela la etimología griega (de geo, tierra; metrein, medir).
La necesidad de medir la tierra para repartir los campos con exactitud dio nacimiento a esta ciencia.
El término latino agrimensura tiene la misma significación, pero el desarrollo posterior de la geometría, como ciencia teórica, obligó a reservar el concepto de agrimensura a la técnica que se ocupa de la medición de los terrenos.
Los más antiguos estudios de geometría fueron hechos por los antiguos caldeos y egipcios.
Los primeros, aunque no sistematizaron sus estudios, obtuvieron algunos resultados correctos, y los segundos hicieron grandes, progresos, como lo demuestra la construcción de las pirámides consideradas hoy como una de las maravillas del mundo.
Los egipcios fueron los primeros que usaron la geometría para medir los terrenos.
El Nilo, río que atraviesa su territorio, se desborda todos los años provocando grandes inundacio nes, que son aprovechadas en la fertilización de los campos.
Los egipcios se veían obligados después de cada inundación a efectuar mediciones para delimitar los campos y terrenos.
Era muy importante para ellos marcar las esquinas de los terrenos en ángulo recto y conocieron prácticamente algunas de las relaciones entre los lados de los triángulos rectángulos.
La verdadera fundación de la geometría como ciencia independiente, sobre bases rigurosas, corresponde a los griegos Pitágoras, Euclides, Arquímedes y Apolonio.
Una imagen de una obra de Durero explicando la proyección geométrica, aplicada en los dibujos y obras de arte
Pitágoras, nacido en el siglo VI antes de Jesucristo, de extraordinario talento matemático, descubrió la relación existente entre los lados de un triángulo rectángulo cualquiera, aunque el teorema que lleva su nombre ya era conocido de los chinos y egipcios.
Dicho teorema se enuncia así: "En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados".
Euclides escribió un libro llamado Elementos, en el que da las bases de un sistema geométrico que se mantuvo en vigencia durante veinte siglos y que todavía constituye el fundamento de la geometría en la enseñanza media.
Partiendo de ciertas proposiciones indemostrables, llamadas postulados, Euclides funda todas las demostraciones posteriores.
De todos los postulados, el más famoso es el V, llamado de las paralelas, pues todo su sistema descansa sobre la evidencia del mismo.
Dicho postulado ha sido la preocupación de todos los matemáticos, quienes en un tiempo, negando que pudiese ser aceptado sin demostración, lo discutieron,ya en el sentido de negarlo, ya en el de probarlo, hasta que la labor crítica del siglo XIX estableció que era indemostrable.
Otro pilar de la matemática griega, Arquímedes, de la ciudad de Siracusa, muerto por los soldados romanos cuando ocuparon esta ciudad en el 212 antes de Jesucristo, planteó nuevos problemas, determinó, con mayor exactitud que la obtenida hasta entonces, la relación existente entre la circunferencia y el diámetro, estableció el volumen de los cuerpos limitados por superficies curvas, inventó la espiral que lleva su nombre y sentó las bases del cálculo integral.
Arquímedes fue un verdadero genio de la matemática; famoso además por la cantidad de aparatos que inventó para la defensa de Siracusa.
Fue muerto por un soldado al no recibir respuesta a preguntas que éste le dirigía, por estar absorto en sus meditaciones.
El general romano Marcelo, que había dado orden de respetar las vidas de los siracusanos, sintió profundamente la pérdida del gran geómetra y ordenó le diesen digna sepultura e hizo grabar sobre su tumba una esfera inscrita en un cilindro, en memoria de uno de sus más famosos descubrimientos.
El cuarto gran geómetra griego es Apolonio de Pérgamo, que floreció a fines del siglo n antes de Jesucristo.
No sistematizó los conocimientos anteriores a él, como Euclides, ni abarcó tanta diversidad de temas como Arquímedes, sino que orientó sus esfuerzos en una dirección única, dedicándose exclusivamente al estudio de las secciones cónicas, con tal profundidad, que sólo en tiempos muy recientes se ha podido añadir algo a lo descubierto por él.
Debían pasar más de 1900 años para que la geometría tomara otro gran impulso. Descartes, filósofo y matemático francés del siglo XVII, estudia las figuras geométricas refiriéndolas a un par de coordenadas.
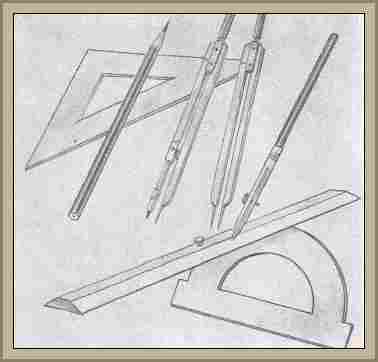
Herramientas basicas para estudiar geometría en el plano: regla, escuadra y compás.
La geometría analítica desarrollada por Descartes es, en síntesis, la reducción de la geometría al álgebra; por ejemplo, la posición de un lugar cualquiera de la superficie terrestre queda determinada por su longitud y su latitud, o sea, por su distancia al Ecuador y a un meridiano.
Análogamente se fija la posición de un punto en un plano por sus distancias a un par de ejes perpendiculares entre sí, llamados eje de las abscisas el horizontal, y de las ordenada el vertical.
En la geometría analítica los puntos quedan determinados en el plano por una pareja de números —sus coordenadas,— y las figuras geométricas se pueden estudiar por medio de ecuaciones.
El siglo XVIII señala el nacimiento de la geometría descriptiva con Monge, matemático francés que perfecciona ensayos anteriores de otros geómetras y da los fundamentos básicos de esta disciplina.
La geometría descriptiva es la representación, sobre superficies planas, de cuerpos que ocupan un lugar en e) espacio; esta representación se efectúa mediante operaciones gráficas regidas por leyes que Monge dedujo.
Dos grandes matemáticos del siglo XIX, el ruso Lobachewski y el húngaro Bolyai, trabajando independientemente, publicaron al mismo tiempo el resultado de sus trabajos de investigación, en los que llegan a las mismas conclusiones.
Estos resultados fueron un acontecimiento de importancia extraordinaria en la historia de la geometría, pues dieron origen a las geometrías no euclidianas, que prescinden del postulado V y llegan a construir un encadenamiento lógico tan riguroso como el del genio griego.
Gracias a ellos fue posible resolver problemas desconocidos para Euclides.
La aparición de las geometrías no euclidianas. dio como resultado un enorme progreso no sólo en la matemática, sino también en la física. E
n ellas se basan algunas de las conclusiones de la teoría de la relatividad de Einstein.
Algunos términos usados en geometría. La geometría trabaja con hipótesis, definiciones y teoremas.
No podemos iniciar un razonamiento en tanto no tengamos ciertas verdades sobre las cuales basarlo; Euclides llamó axiomas a ideas o razones tan evidentes que no necesitan demostración, tales como "una cosa es igual a sí misma"; y postulados, a verdades no tan evidentes como los axiomas, pero que también se aceptan sin demostrar ("por un punto pasan infinitas rectas", y "entre dos puntos puede trazarse una sola recta").
Las hipótesis son proposiciones que se pueden considerar como verdades que es necesario demostrar: la hipótesis puede ser falsa y entonces nos lleva a falsas conclusiones.
La hipótesis y las consecuencias que se derivan de ella perduran hasta que se demuestre su inexactitud.
Así, la hipótesis de que la Tierra era plana, generalizada desde hacía siglos hasta los tiempos de Colón, no fue definitivamente abandonada hasta que los viajes y descubrimientos efectuados por portugueses y españoles, en los siglos XV y XVI, la desvirtuaron, y el arribo de Elcano a España, después de haber sido el primero que dio la vuelta al mundo, estableció irrefutablemente la redondez del planeta.
Las definiciones sirven para caracterizar las figuras que se van a estudiar; deben ser precisas, para poder basar nuestro razonamiento sobre ellas y no deben contener más que lo que se quiere definir.
No podemos estudiar, por ejemplo, los triángulos, si previamente no hemos definido con exactitud qué entendemos por un triángulo.
Si examinamos una definición como: "un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos", vemos que comienza por separar todo lo que no se refiera a una figura de cuatro lados, luego a todas aquellas cuyos lados no son paralelos, lográndose así que la definición se refiera a un paralelogramo y nada más que a él.
El teorema es una exposición formal, que hay que demostrar mediante su mecanismo lógico y consta de dos partes; la hipótesis, que establece lo que va a ser probado como verdad, y la tesis, que es la consecuencia del razonamiento lógico que se ha seguido para demostrar la hipótesis.
• Elementos.
En la geometría hay ciertos elementos fundamentales: el punto, la recta y el plano.
El punto no tiene dimensiones y puede ser representado por la señal que deja la punta de un lápiz sobre el papel o por una cruz, en la que la intersección de las líneas marca el lugar del punto.
La recta tiene una sola dimensión, longitud; el hilo tenso de la plomada da una idea de ella.
El plano tiene dos dimensiones, largo y ancho.
La superficie de una mesa, las aguas en reposo, nos dan una representación del plino.
Con estos elementos se construyen las figuras —triángulos, cuadriláteros, círculos—, que son rectilíneas si sus lados son rectas, o curvilíneas si son curvas.
La geometría plana se refiere a estas figuras de dos dimensiones: la geometría del espacio se refiere a los sólidos que tienen tres dimensiones —ancho, alto y profundidad—, como cubos, esferas, conos, naralelepínedos, etcétera.
La geometría, considerada desde un punto de vista estrictamente matemático, es la ciencia que se ocupa de las relaciones entre cuatro magnitudes simples: longitud, latitud, profundidad y abertura angular, y dos compuestas: superficie y volumen.
UN COMPLETO CURSO DE GEOMETRIA ELEMENTAL PARA LOS PRINCIPIANTES
 |
1-Elementos de Geometría Plana |
|
|
|
2-Triángulos |  |
|
|
3-Cuadriláteros | |
|
|
4-Polígonos | |
|
|
5-Circunferencia y Círculo | |
|
|
6-Perímetros y Áreas | |
|
|
7-Semejanzas | |
|
|
8-Geometría del Espacio | |
|
|
9-Poliedros | |
|
|
10-Cuerpos de Revolución | |
|
|
11-Áreas y Volúmenes | |
|
|
12-Movimientos en el Plano | |
|
|
13-Trigonometría | |
|
|
14-Geometría Analítica | |
Temas Enlazados al Sitio Oficial: CNICE (Ministerio de Educación y Ciencias)
Temas Curiosos Relacionados:
Geometria Panal de Abejas Celda Hexagonal de los Panales
Espacios Sagrados: Concepto y Geometria Sagrada
El Pentragrama o Estrella de Cinco Puntas-El Simbolo del Priorato
Origen del Numero de Cero
Enlace Externo:• Dura Creatividad: El origen de la geometría
