Biografia de Pitagoras,Matematico Griego:Vida y Obra Cientifica
Biografia de Pitágoras Matemático Griego Vida y Obra Cientifica
Seis siglos antes de Cristo, aparece una nueva cultura que cambia el rumbo de las matemáticas, la cultura griega. Uno de sus grandes sabios crea una escuela que sienta las bases de esta ciencia a traués del estudio de los números y sus relaciones.
El hombre que creó la tabla de multiplicar (ver Tabla Pitagórica) fue Pitágoras, contemporánea de Buda y Confucio, que nació en la isla griega de Samos hacia 582 a.C.
De su vida, envuelta en la leyenda, se sabe que, huyendo de la tiranía de Polícrates, abandonó Samos y se instaló en una colonia griega del sur de Italia, la próspera Crotona.
Allí fundó una escuela filosófica cuyos seguidores creían que el Universo se apoyaba en los números y que éstos influían en los hombres. Su emblema era «Todo es número».

SU BIOGRAFIA
PITÁGORAS (569 a.C - 495 a.C.): Filósofo y matemático griego del siglo VI antes de J.C. No existen
Fundador de la secta de los pitagóricos.
Exigía de sus discípulos y de sí mismo una vida absolutamente austera.
Estudió las propiedades físicas a las cantidades y magnitudes, empleando como fundamento de todas sus teorías la ciencia de los números
Se le atribuye la invención de la tabla de multiplicación o pitagórica , y de un sistema de geometría del que formaba parte el famoso teorema de Pitágoras, sobre los lados de un triángulo rectángulo.
Se le atribuye a la secta de los pitagóricos una suerte de religión basada en las propiedades místicas de los números.

Pitágoras, maestro y fundador de una orden en Crotona, en el sur de Italia, fue uno de los padres de la filosofía, concebida como el conocimiento total del universo. Pitágoras marcó el pensamiento de la Antigüedad hasta fines del Imperio romano.
La biografía tradicional de Pitágoras nos lo describe como natural de Samos, hijo de un tal Mnesarco, aunque en ciertos momentos se ha llegado a dudar de la realidad de la existencia de Pitágoras, sin embargo, existen algunos indicios que prueban la vida histórica de Pitágoras, a quien impropiamente se ha llamado padre de las matemáticas y fundador de la doctrina filosófica de los números.
Esta parte de la personalidad de Pitágoras ha de atribuirse a los hombres de su escuela, agrupados en una comunidad parecida a las sociedades secretas modernas.
Muchas de sus ideas eran difíciles de digerir a causa de su extravagancia.
A sus seguidores les prohibió comer judías, argumentando que si enterrabas una judía durante cuarenta días cubriéndola con estiércol, adoptaría una forma humana.
Creía en la transmigración de las almas, así que, según él, el alma de un hombre en una existencia anterior bien había podido habitar en el cuerpo de una medusa.
Pero si las especulaciones de Pitágoras condujeron a sus discípulos un pantano de supersticieones , su perspicacia en matemáticas y astronomía hizo que los científicos posteriores estuvieran en deuda con él.
Fue Pitágoras el que hizo de las matemáticas un sistema lógico unificado, en vez de un conjunto de reglas para casos especiales.
También fue el primero, que sepamos, que especuló con que la Tierra pudiera tener una forma esférica; ni los babilonios, ni los egipcios, ni los primeros griegos habían sido conscientes de la verdadera forma de la Tierra.
Homero creyó que era un disco convexo, rodeado por un río.
Algunos contemporáneos creyeron que tenía forma de plato, que se apoyaba en cuatro elefantes de pie sobre una tortuga.
CONSIDERADO COMO UNO DE LOS SIETE SABIOS DE GRECIA
Ver: Tabla Pitagorica
Ver: Los Siete Sabios de Grecia
Recibió una cultura dilatada, y entre sus maestros contó a Anaxágoras.
Ya mayor, sus viajes — sobre los que existen dudas fundamentadas —, le llevaron a Egipto y quizá a Babilonia, donde aprendió los secretos de la vida religiosa y del cálculo matemático de aquellos pueblos.
De regreso a su país natal, lo halló bajo el poder del famoso Polícrates.
Entonces decidió emigrar de Samos.
Acaso hacia 30 pasó a la Magna Grecia.
En Crotona fundó su primera comunidad religiosa, la cual alcanzó pronto gran difusión.
Pero habiendo surgido discrepancias en su seno, Pitágoras se trasladó a Metaponto, donde le sorprendió la muerte a principios del siglo v antes de nuestra Era.
La liga pitagórica se basaba en una creencia religiosa, que probablemente su fundador adoptó de los misterios órneos.
En efecto, Pitágoras creía en la transmigración de las almas, doctrina de sentido ético que interpretaba la reencarnación como castigo o recompensa de una existencia anterior.
En este sentido, discrepaba profundamente de la religión de los poetas, con sus dioses arrebatados y poco serios.
A los miembros de la comunidad les exigía una rigurosa sumisión a la autoridad, la abstención de todo goce sensible y, en general, de los bienes exteriores; la privación de ciertos manjares, entre los cuales la carne, y, en la vida política, una actitud aristocrática y conservadora.
Aparte esta actividad religiosa fundamental, Pitágoras cultivó las matemáticas y la música.
En este aspecto fue básico su descubrimiento de que la altura de los sonidos depende de la longitud de la cuerda vibrante, de lo que nació la idea de que la realidad del mundo se hallaba estructurada por una regularidad.
La formulación de esta doctrina tuvo derivaciones fecundísimas, a pesar de las inevitables desviaciones fantásticas.
Pitágoras o los pitagóricos creyeron en la esfericidad de la Tierra y en su movimiento alrededor de un fuego central en una colosal armonía celeste.
A Pitágoras se le atribuye La invención de las palabras Filosofía (amor por la sabiduría y Matemática lo que se aprende, un matemático es el que aprende).
Inventó estas palabras para describir sus actividades intelectuales.
Además, consideraron las matemáticas como prototipo del conocimiento exacto y seguro, y las elevaron por encima de las simples necesidades comerciales.
Respecto al famoso «teorema de Pitágoras», baste decir que ya lo conocían los egipcios y los mesopotámicos.
El Teorema de Pitágoras:
Se cuenta que, cuando dio con la demostración del teorema que lleva su nombre, Pitágoras hizo sacrificar un buey en la escuela para celebrarlo.
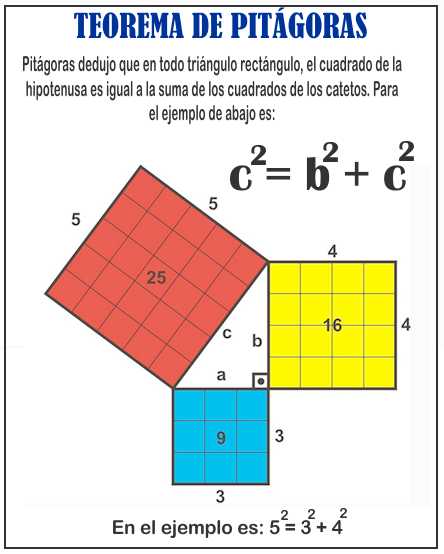
El teorema postula que en todo triángulo con un ángulo recto, el cuadrado de la hipotenusa (el lado largo) es igual a la suma de los cuadrados de los catetos (arriba).
Dicho de otro modo, si los lados de un triángulo rectángulo tienen longitudes a, b y c, y c es el más largo de los lados, entonces a² + b² = c².
Existe un número infinito de soluciones integrales a esta ecuación, o valores para a, b y c, que son números enteros. Los ejemplos más sencillos de estas «temas pitagóricas» son (3, 4, 5) y (5, 12, 13).
Inspirado por su teoría filosófica de los números, Pitágoras realizó numerosas investigaciones en las matemáticas.
Sí bien se le atribuye el descubrimiento de numerosos teoremas, algunos pertenecen a sus discípulos del siglo V a.C.
Además del famoso «teorema de Pitágoras» (sobre el cuadrado de la hipotenusa), los pitagóricos formularon la primera teoría sobre las proporciones, la clasificación de los números, el descubrimiento de los números irracionales y las tablas de multiplicación o el sistema decimal.
Cuando Pitágoras descubrió su famoso teorema, agradeció a los dioses sacrificando un buey, hecho de pasta, siendo fiel a sus convicciones filosóficas.
Para Pitágoras entre los números y los dioses existía una maravillosa y misteriosa relación, en la que se basaba la ciencia de la aritmancia o la magia procesal.
Uno de sus seguidores, convirtió en palabras esta teoría:
"Antes de los números matemáticos se encuentran los números animados."
Otro historiador escribió:
"Los números de Pitágoras hemos de verlos como unos símbolos jeroglíficos, por medio de los cuales se representaba la totalidad de las ideas relacionadas con la auténtica naturaleza de las cosas."
Se sabe que los antiguos sabios concedían un doble sentido a los números, y los pitagóricos se hicieron famosos en todo el mundo por servirse de esta teoría.
No obstante, en el segundo aspecto de tan singular ciencia, al exacto conocimiento de los números animados sólo accedían los iniciados.
Este poder era revelado a los más puros, al creer que su sentido universal y su simbología no debía vulgarizarse.
Adquirían el derecho a conocerlos aquellos que habían superado las cuatro pruebas fundamentales del óctuple sendero.
Esto les permitía adquirir una fuerza superior y el grado más elevado de la virtud.
ALGUNAS PROPIEDADES DESCUBIERTAS DE LOS NUMEROS NATURALES
Los números perfectos:
Hay un hermoso libro sobre las matemáticas llamado "El Hombre Que Calculaba" de Malba Tahan donde Beremiz Samir narra a su acompañante curiosas y enigmáticas historias que finalmente se resuelven aplicando la matemática.
En una de esas historia explica lo que son los número perfectos, de la siguiente manera:
- El número 496 es un número perfecto
- ¿Y qué quiere decir un número perfecto?, preguntó el poeta. ¿En qué consiste la perfección del número?
- Número perfecto, explicó Beremiz, es el que presenta la propiedad de ser igual a La suma de sus divisores, excluyéndose, claro está, de entre ellos el propio número. Así, por ejemplo, el número 28 presenta 5 divisores menores que 28; 1, 2, 4, 7, 14
La suma de esos divisores es precisamente igual a 28. Luego 28 pertenece a la categoría de los números perfectos.
El número 6 también es perfecto. Los divisores de 6, menores que 6, son : 1, 2, 3, cuya suma también es 6. Al lado del 6 y el 28 puede figurar el número 496, que también es perfecto.
Los números triangulares:
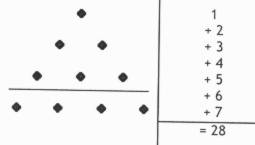
Los números triangulares se generan a partir de la serie de tos números naturales puestos en línea, y por continuas adiciones de los términos sucesivos, uno a uno, desde el principio, de manera que por sucesivas combinaciones y adiciones de otro término a la suma, los números triangulares se van completando en orden regular.
Los números triangulares son, pues, suma de La serie de Los naturales hasta uno determinado: Por ejemplo 28 = 1 + 2 -e- 3 + 4 + 5 + 6 + 7. Por eso decimos que el 28 es número triangular de lado 7.
En lo que sigue designaremos abreviadamente Los números triangulares con eL número de que se trate seguido de su lado entre paréntesis. Así eL 28, que es número triangular de lado 7, se expresara como 28(7).
Otros números triangulares son: 120(15), 153(17), 276(23), 666(36).
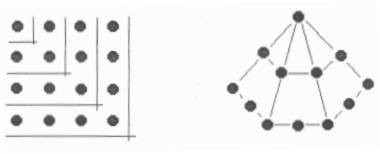
Los números cuadrados y pentagonales:
El concepto es similar al de tos números triangulares. El 1, 4, 9, 16, el 25, ... son números cuadrados, eL 1, 5, 12, 22, 35, ... son números pentagonales.
Números Amigos:
Cada uno de ellos es igual a la suma de los divisores propios del otro, por ejemplo el par 220 y 284.

Observese que los divisores del 220 son: 1,2,4,5,10,11,20,22,44,55,110, que sumandos dá 284.
Los divisores del 284 son: 1,2,4,71,142 que sumando dá: 220
Entonces el 220 es amigo del 284.
Música y Números:
Uno de los logros más notables de su escuela fue el descubrimiento de la base matemática de los tonos musicales.
Mucha gente habrá notado que una cuerda corta emite una nota más alta que una larga.
Pues bien, fue Pitágoras el que descubrió la relación matemática entre la longitud de una cuerda y la nota que emite, de forma que si se dobla la longitud de la cuerda, el sonido disminuye una octava; si la proporción de las longitudes es de tres a dos, la diferencia en el tono es de una quinta parte, y así sucesivamente.
Se dice que Pitágoras era un notorio melómano (que siente pasión y entusiasmo por la música.).
Se decía que al pasar por una herrería quedó intrigado por las notas que y producían los distintos martillos sobre el yunque; investigó las notas producidas al pulsar cuerdas tensadas e inventó la escala musical sobre bases matemáticas.
Aunque se trata de un relato improbable, como es casi seguro que estudió música en Egipto, quizá experimentara con cuerdas tensadas y a partir de ello formalizara la escala musical de modo matemático.
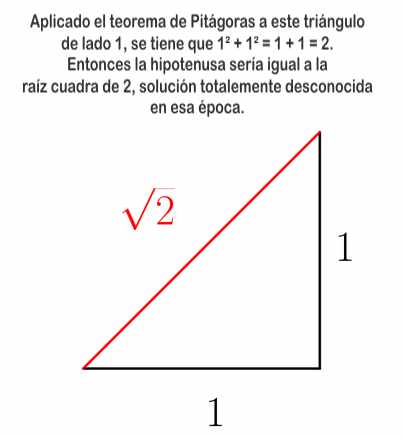
Pitágoras creía que todo era susceptible de ser descrito empleando números enteros, pero en un triángulo rectángulo cuyos catetos midan ambos uno, la longitud de la hipotenusa se obtiene por la raíz cuadrada de dos.
Hipaso, uno de los matemáticos de la escuela, logró demostrar geométricamente que la raíz cuadrada de dos es un número irracional: no puede representarse como razón aritmética o fracción p/q, donde p y q son números enteros.
Hay quien cree que Hipaso fue arrojado por la borda de un barco y se ahogó; otros dicen que el disgusto de Pitágoras fue tal que se suicidó.
En cualquier caso, la raíz cuadrada de dos es irracional; escrita como decimal se escribe de este modo: 1,414213562373095... y continúa infinitamente sin patrón alguno.
Ver Demostración Pitagórica Del Número Irracional Raíz de 2
LA ESCUELA DE PITÁGORAS EN CROTONA
Debido a sus enseñanzas, Pitágoras logró un inmenso prestigio en todo el sur de Italia, y sus discípulos fundaron varias heterías pitagóricas en distintas ciudades de la Magna Grecia.
Su doctrina se difundió ampliamente gracias a los cursos dictados a oyentes libres, los «exotéricos».
Un halo de magia rodeaba al Maestro, poseedor según algunos de los dones de ubicuidad y profecía.
También se decía que hablaba con los ríos y los animales.
Tal irradiación tuvo implicancias políticas.
Como su visión planteaba que la sociedad debía reflejar la estructura jerarquizada del universo, Pitágoras apoyaba el partido aristocrático.
Ejerció una profunda influencia en el gobierno de Crotona y, por medio de sus discípulos, en el de varias ciudades itálicas.

La escuela de Pitágoras: En el sur de Italia, Pitágoras fundó una hermandad mística para la que «todo es número».Los malemálicos vivían de forma permanente en esta peculiar institución, y a los oyentes se les permitía asistir durante el día
ULTIMOS AÑOS DE PITAGORAS:
Parece que los habitantes de Crotona se cansarían de la vecindad de aquella colonia de místicos y sabios, cuya influencia, aun sin ellos quererlo, tenía que ser imponderable.
Un novicio que había sido expulsado se aprovechó de un momento de disgusto popular para atribuir los males de Crotona a los pitagóricos y, amotinada la gente, puso fuego a la colonia con todos los que en él habitaban.
Una tradición dice que el maestro pudo escapar y que acabó sus días en Metaponto.
Otra tradición asegura que sólo se salvaron dos iniciados, Arquipos y Lisis, que esparcieron la nueva doctrina por todo el mundo griego.
Pero ya Aristóteles insiste en la distinción entre Pitágoras y los pitagóricos para indicar que la doctrina del filósofo de Samos era diferente de la de sus discípulos.
De todos modos, parece imposible absolver a Pitágoras del pecado de magia y de exagerados escrúpulos de moral; impuso a sus discípulos largos períodos de silencio y abstinencia, y los catecúmenos sufrían penosas iniciaciones para llegar al conocimiento superior, siendo purificados con catarsis, o purificaciones musicales, que limpiaban el alma como las purgas el cuerpo.
En la escuela de Crotona se creía en la reencarnación y en la fraternidad de hombres y animales.
Pero también los antiguos hubieron de reconocer los grandes progresos que en casi todos los ramos de la ciencia se consiguieron por el esfuerzo de Pitágoras, especialmente en la geometría, la música y la astronomía.
Hoy parece probado que el primer libro de los Elementos, de Euclides, que ha sido la base de las geometrías elementales hasta la época moderna, es, en sustancia, obra de Pitágoras.
El pensamiento pitagórico ejerció su influencia en la filosofía hasta fines de la Antigüedad, tanto es así que los últimos grandes pensadores del Imperio romano se autodenominaron «neopitagóricos».
Acerca de la muerte de Pitágoras existen las mismas dudas que sobre el resto de mi vida.
Hay quien dice que falleció como consecuencia de uno de los mencionados episodios de rebeldía, cuando su casa fue arrasada.
Otras fuentes afirman que logró huir a Tarento, en el sur de Italia, y que pocos años después murió asesinado en otra revuelta popular en Metaponte, Lucania.
No faltan los autores que mencionan una muerte tranquila, acaecida en Crotona entre los años 505 y 500 a. C.

SOBRE LOS NÚMEROS IRRACIONALES...
Pitágoras observó que la raíz cuadrada del número no podía expresarse mediante una fracción, es decir, que no es un número racional, y además, como de acuerdo con el teorema de Pitágoras la hipotenusa de un triángulo rectángulo de catetos b y c está dada directamente por la raiz cuadrada de (b2 + c2), los matemáticos de la escuela pitagórica observaron que esa expresión en la mayoría de los casos no es un número racional.
Este descubrimiento de Pitágoras se festejó con el sacrificio de 100 bueyes.
Los matemáticos griegos posteriormente estudiaron, además de estos números irracionales sencillos, otros más complicados, pero siempre resultados de la extracción repetida de raíces cuadradas.
Así se llegó a tener la idea de número irracional, pero esta idea se generaliza recién al final del siglo XVI con la introducción de números decimales, pues cuando se transforma una fracción en número decimal puede presentarse el caso que dé un número de infinitas cifras.
El ejemplo más sencillo es el de la fracción que da por resultado el número 0,3333 ....., y muchas como éstas que son las conocidas expresiones periódicas; pero ya entonces no fue difícil aceptar o hacerse a la idea de otros números decimales de infinitas cifras pero no periódicos y cuyo orden de aparición no responde a ninguna ley determinada, o sea el número irracional.
Como bien se sabe, entre los números irracionales hay dos fundamentales en la matemática, que son el número π y el número e.
Desde el momento en que en la antigua Mesopotamia, unos 6.000 años a. de J. C, un desconocido ciudadano descubrió la rueda, descubrimiento que más influyó en el avance de la civilización y de la industria, se le planteó al hombre el problema de la determinación de la longitud de la circunferencia y de la superficie del círculo, y estos problemas llevaron a la determinación o cálculo de la razón entre la circunferencia y el diámetro, o sea el número ir.
Se calcularon valores aproximados de este número, y así: Los pueblos mesopotámicos habían considerado para n el valor poco aproximado pero muy cómodo: 3.
Arquímedes lo expresó aproximadamente por la fracción 22/7 , que da un valor con un error menor que 2 milésimos.
Adriano Metus expresó el valor de e aproximadamente por la fracción 355/113 que da su valor con error menor que 1 millonésimo.
Hace unos cien años el inglés Shanks logró calcular π con 700 cifras decimales. Este trabajo, que le llevó largos años de labor, sólo es interesante desde el punto ilustrativo, pues: primero, para las aplicaciones nunca se consideran tantas cifras; y, segundo, las máquinas de calcular que posteriormente obtuvieron muchas más cifras decimales de π señalaron un error en una de las cifras calculadas por Shanks.
La gran importancia de los números irracionales se pone de manifiesto en que aparecen en la gran mayoría de las fórmulas y expresiones que permiten la resolución de problemas de la física, en particular de la radio y de las máquinas de precisión.

La belleza como meta:
pitágoras entendía la belleza, en su sentido humano, como la exaltación del individuo hasta su propia perfección.
Para conseguirla debía servirse de dos elementos complementarios: el desarrollo total de sus facultades físicas, morales e intelectuales, y procurando imitar el modelo divino.
Como creían todos los iniciados griegos, el ser humano dispone en su interior de la simiente de esa belleza.
Por medio de ciertas técnicas pedagógicas se podía conseguir extraerla y, luego, desarrollarla de la forma más positiva.
Era muy consciente el Sabio de Samos que con el cultivo armónico de todas las facultades físicas e intelectuales, el hombre y la mujer podían perfeccionarse, empezando por la belleza del cuerpo.
El filósofo alejandrino Plotino lo definió de esta manera:
Retírate para conseguir examinar tu interior y no dejes de contemplarte. En el caso de que no te considerases demasiado bello, procura imitar al creador de una estatua: observa el modelo de la belleza para reproducirlo sin el menor error.
Para lograrlo elimina trozos de mármol, pule ciertas zonas, suaviza una línea, completa otra y no se detiene hasta alcanzar la meta deseada: la perfecta reproducción.
Como él ha actuado, abandona lo inútil, pon derecho lo torcido, da luz a las sombras y nunca dejes de cincelar la estatua que es tu propio cuerpo.
Debes perseguir que sobre ti resplandezca el divino fulgor de la virtud, para así poder certificar que la divinidad se halla presente en el santuario que forman tu cuerpo y tu mente.
Pero la belleza también podía encontrarse en la palabra, ya que tenía mucho de música.
Pitágoras recomendaba: Habla sólo cuando la palabra valga más que el silencio. Concederemos un mayor valor a esta frase clave si tenemos en cuenta que el Iniciado fue llamado el "Hijo del Silencio".
Por lo que afecta a la belleza corporal, sabía de antemano el Maestro de Samos los secretos de su lenta configuración.
Se obtenía por medio de ciertos ejercicios físicos, un ambiente artístico, los conocimientos que concedían mayor importancia a lo espiritual que lo material y algunos controles alimenticios.
La leyenda refiere que Pitágoras aprendió en Egipto, Persia y Babilonia a manipular el agua como si fuera una lira.
Conocía los secretos para armonizar las fuentes, graduar el sonido delicado de la brisa en los jardines, cultivar el canto de los pájaros amaestrados y tañer una serie de instrumentos de Asia, de África y de Europa, propicios a la armonización de los gestos a través de la danza.
Pero la danza no formaba parte de las enseñanzas que recibían esos primeros veintiocho alumnos, aunque sí de los otros miles que llegarían más tarde, en diferentes lugares de Grecia e Italia.
Entonces se comprobaría que el baile místico, aunque fuese practicado individualmente por hombres y mujeres, todos ellos pitagóricos, ayudaba a la belleza del cuerpo humano.

CRONOLOGÍA DE LA VIDA PITÁGORAS
c.569 a.c. Pitágoras nace en Samos, en la isla del mismo nombre, hijo de Mnesarco y Pitáis. Su ciudad natal fue renombrada Pitagorlo en su honor.
c.550 a.c. Viaja a Mileto y estudia con Tales, uno de los primeros filósofos griegos (y astrónomo que al parecer predijo un eclipse de sol en 585 a.C), y con el discípulo de Tales, Anaximandro, interesado por la cosmología y la geometría.
c.535 a.c. Por consejo de Tales viaja a Egipto, donde vive una Importante comunidad oriunda de Samos que dispone incluso de un templo propio en Náucratls. Pitágoras estudia astronomía y geometría.
c.525 a.c. Se cuenta que es hecho prisionero y llevado a Babilonia por el rey persa Camblses II. Allí estudia aritmética, música y otras disciplinas con los sabios.
c. 520 a.c. Regresa a Samos, donde funda su escuela tras una visita a Creta para estudiar su sistema legal. Sin embargo, no es bien tratado en Samos y parte a la Grecia continental, y de allí al sur de Italia.
c. 518 a.c. Pitágoras se establece en Crotona, un puerto de población griega en la Magna Grecia (sur de Italia), y funda una escuela o hermandad dedicada al estudio de las matemáticas, pero que Incluye también una escuela de medicina. Los pitagóricos juran no revelar sus secretos y siguen normas curiosas: no se les permite comer carne, pescado ni legumbres, ni beber vino. Tienen prohibido vestir prendas de lana, por su origen animal. Ello puede deberse a la creencia de Pitágoras en la reencarnación y en la posibilidad de nacer de nuevo como animal.
c.510a.c. La atípica hermandad pitagórica despierta hostilidad y desconfianza; ante la amenaza de violencia, Pitágoras decide huir a Metaponte, otra ciudad griega del sur de Italia.
c.495 a.c. Muere en Metaponte.
Fuente Consultada:
PITÁGORAS Grandes Iniciados Patricia Caniff
Matematica Moderna Aritmética de 2º Año Repetto-Linskens-Fesquet
Ver: Biografia de Thales de Mileto
Ver: La Ciencia en Grecia Antigua
Notación Complementaria
Isla de Samos está ubicada al sureste de Grecia, en el mar Egeo, cercana a la costa de Turquía.
Mesaponto, Ciudad del sur de Italia.
Buda (c. 563-c. 486 a.C.), fundador del budismo, nacido en el parque Lumbini cerca de Kapitavastu, en la actualidad Nepal, cerca de la frontera india.
Confucio, en chino Kongfuzi (c. 551-479 a.C.), filósofo chino, creador del confucionismo y una de las figuras más influyentes de la historia china. Loo-Tsé o Laozi (c. 570-c. 490 a.C.), filósofo chino considerado el fundador del taoismo.
Tiro, ciudad del sur del Líbano, junto al mar Mediterráneo.
Magna Grecia, nombre dado en la antigüedad a las colonias griegas del sur de la península Itálica.
Antigua ciudad griega de Jonia, en la costa oeste de Asia Menor (parte de la actual Turquía).
Cambises II, rey de Persia (529-522 a.C.), hijo de Ciro II el Grande, a quien sucedió, Para mantener el control sobre el Imperio persa, Cambises II asesinó a su hermano menor, Smerdís (c. 523 a.C.). Después encabezó una expedición contra Egipto.
Babilonia, una de las ciudades más importantes de la antigüedad, cuya localización está hoy en día marcada por una amplia zona de ruinas al este del río Éufrates, a 90 km al sur de Bagdad, en Irak.
Darío I el Grande (c. 558-486 a.C.), rey de Persia (c. 521 - 486 a.c.)







