Cálculo del Radio de la Orbita en el Átomo de Hidrógeno
Cálculo del Radio de la Primera Órbita del Átomo de Hidrógeno
Como es sabido, un átomo puede compararse a un sistema solar en miniatura.
El centro, o núcleo, es relativamente pesado y estacionario, mientras que los electrones giran alrededor, en forma similar a como los planetas giran alrededor del Sol.
En general, las distancias electrón-núcleo son del orden de 10-8 cm, 0,00000001 cm.
Esquema Atomo del Hidrogeno
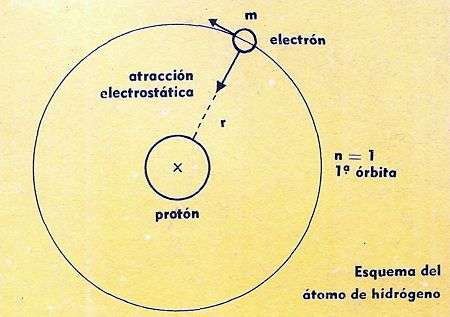
En un átomo la fuerza que mantiene a los electrones en sus órbitas no es gravitatoria, sino de naturaleza electrostática, ya que el protón (único componente del núcleo en el átomo de hidrógeno) y el electrón tienen cargas contrarias.

Al igual que la fuerza gravitatoria, la electrostático es inversamente proporcional al cuadrado de las distancias.
Teniendo en cuenta que en una órbita circular la fuerza centrípeta está constituida por esta fuerza de atracción electrostática, e introduciendo el postulado de Niels Bohr, que establece que el momento angular del electrón en una órbita circular está cuantificado, es decir, sólo puede alcanzar valores enteros de h/2.¶ , donde h es la constante de Planck, obtendríamos la siguiente expresión:
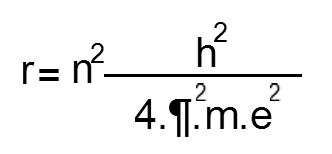
que nos permite hallar para la distancia requerida el valor de 5.28.10-9 cm., sustituyendo las constantes n (en este caso es igual a 1, por ser la primera órbita), h (constante de Planck), m y e (masa y carga del electrón) por sus valores respectivos.
Valores de:
h=6.62606957 ×10 -34 J×s
m=9,109 382 91×10−31 Kg.
e=1,602 × 10-19 culombios
El valor obtenido, conocido como radio de Borh es: 5,291 772 0859×10−11 m.






