Fórmulas de Volumenes de Cuerpos Geométricos:Tabla Online
FÓRMULAS DE VOLUMEN DE CUERPOS GEOMÉTRICOS
Los cuerpos geométricos tridimensionales o simplemente cuerpos ocupan siempre un espacio. La medida de ese espacio recibe el nombre de volumen.
Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos (sólidos, líquidos o gaseosos) en una cantidad que recibe el nombre de capacidad. Existe una relación directa entre la capacidad de un cuerpo y el volumen que éste ocupa.

Esta jarra es un cuerpo de forma cilindrica, y es hueco, entonces se habla de capacidad de la jarra, es decir, cuanto líquido puede contener en su interior. Con la fórmula del volumen del cilindo podemos obtener la capacidad de este envase.
Veams ahora las fórmulas mas utilizadas en nuestra vida diaria....
![]()
1-Fórmula Volumen de un Cubo
2-Fórmula Volumen de un Paralelepípedo
3-Fórmula Volumen de un Cilindro
4-Fórmula Volumen de una Esfera
5-Fórmula Volumen de un Cono
6-Fórmula Volumen de un Toro
7-Fórmula Volumen de una Pirámide
8-Fórmula Volumen de un Casquete Esférico
9-Fórmula Volumen de un Prisma
10-Fórmula Volumen de un Elipsoide de Revolución
![]()
Son cuerpos de revolución aquellos cuerpos tridimensionales (tres dimensiones) que se obtienen al hacer girar una figura plana 360" alrededor de un eje que puede ser uno de sus lados o no.
Por ejemplo, si hacemos girar un rectángulo alrededor de uno de sus lados obtenemos un cilindro; si hacemos girar un triángulo alrededor de uno de sus lados, obtenemos un cono; y si hacemos girar una semicírculo alrededor de su diámetro, obtenemos una esfera.
En cambio, si hacemos girar un círculo alrededor de un eje, que se encuentra en el mismo plano que el círculo, exterior a él, la figura que obtendremos es la de un toro (un ejemplo es la figura de un «donut» (figura abajo)

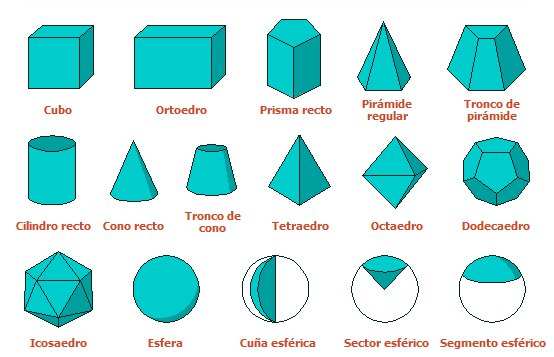
Los cuerpos geométricos existen en el espacio y son, por tanto, objetos tridimensionales limitados por una o varias superficies.
Si todas las superficies que lo limitan son planas y de contorno poligonal, el cuerpo es un poliedro. Los antiguos griegos conocían la existencia de cinco poliedros regulares, cuyo descubrimiento atribuyeron algunos al propio Pitágoras.
Teeteto fue probablemente el autor de la primera construcción teórica rigurosa de dichos poliedros como cuerpos inscritos en una esfera, construcción con la que culminaban los Elementos de Euclides, donde aparece asimismo, como colofón de la obra, la demostración de que sólo pueden existir cinco de ellos.
Pero hay otros cuerpos, como la esfera, el cilindro o el cono, que no están limitados por polígonos, sino por superficies curvadas; son los llamados cuerpos redondos, que también han recibido desde antiguo una atención preferente y cuyas superficies y volúmenes estaban ya recogidos en la obra de Euclides.
Vivimos en un mundo tridimensional. La mayoría de los objetos con los que trabajamos pueden caracterizarse como sólidos tridimensionales.
Todos los cuerpos geométricos tridimensionales, es decir, que tienen un alto, un ancho y una profundidad, ocupan un espacio. La medida del espacio que ocupan dichos cuerpos tridimensionales recibe el nombre genérico de volumen del cuerpo.
El volumen de los cuerpos es aditivo, en la medida en que, si juntamos varios cuerpos de volúmenes V1 ,V2 ,V3 ,el volumen total ocupado por todos ellos es V = V1 + V2 + V3 + ...
Para calcular el volumen de los cuerpos geométricos aprovechamos su forma geométrica, de manera que dividimos el cuerpo en otros cuerpos geométricos más sencillos (cubos, prismas, esferas, etc.) de los cuales conocemos las expresiones matemáticas de sus volúmenes y luego aplicamos la propiedad aditiva del volumen para calcular el volumen total del cuerpo original.
Aunque el volumen de un cuerpo se calcula aprovechando su geometría, esto no quiere decir que los cuerpos que tienen el mismo volumen hayan de tener la misma geometría. Por ejemplo, un cubo y una esfera pueden tener el mismo volumen si elegimos de una forma concreta la arista del primero y el radio del segundo.
La unidad fundamental para el volumen en el Sistema Internacional de unidades (si) es el metro cúbico (m³).
Un metro cúbico corresponde al volumen que ocupa un cubo de arista a 1 m.
Por tanto, resulta que cada unidad de volumen equivale a 1000 unidades del orden inmediatamente inferior (por ejemplo, 1 dm³ = = 1.000 cm³), y que cada 1.000 unidades de un orden equivalen a una unidad del orden inmediatamente superior (por ejemplo, 1.000 hm³ = 1 km³).

FORMULAS DE LOS VOLUMENES MAS COMUNES
► CILINDRO:
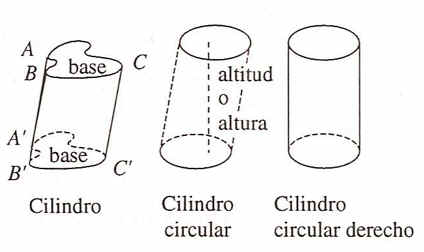
Un cilindro es un sólido cuyos extremos, o bases, son figuras planas paralelas congruentes dispuestas de tal modo que los segmentos que unen los puntos correspondientes en las bases son paralelos. Estos segmentos se llaman elementos.
En el primer cilindro de la figura de abajo AA'. BE' y CC' son elementos del cilindro. Un cilindro circular es aquel en el que ambas bases son círculos.
El cilindro circular recto es el tipo más común de cilindro y se forma cuando las bases son perpendiculares a los elementos. La altura o altitud de un cilindro es un segmento perpendicular a ambas bases.
► PRISMAS:
Como se muestra en la figura de abajo un prisma es un sólido con extremos, o bases, que son polígonos paralelos congruentes con lados llamados caras (o caras laterales) y que constituyen paralelogramos.
Los segmentos que forman las intersecciones de las caras laterales se llaman aristas laterales.
La altura, o altitud, de un prisma es la distancia entre las bases. Un prisma rectangular tiene sus bases perpendiculares a las aristas laterales; por lo tanto, sus caras son rectángulos.

Los prismas reciben sus nombres de las bases. Si las bases son polígonos regulares, entonces se trata de un prisma regular.
El prisma triangular tiene triángulos por bases y el prisma rectangular tiene rectángulos por bases. Los prismas más comunes son los prismas rectangulares rectos, que se llaman paralelepípedos rectangulares, y el prisma cuadrado recto, más conocido como cubo.
Existen dos clases de áreas que suelen asociarse con cualquier figura sólida. El área lateral es la suma de las áreas de todos los lados.
El área superficial total es el área lateral más el área de las bases.
A causa de que la superficie lateral de un prisma recto o de un cilindro recto puede desdoblarse para formar un paralelogramo si se le corta a lo largo de un elemento, el área lateral L se halla multiplicando el perímetro o la circunferencia de la base por la altura. El volumen de un cilindro de un prisma es el área de la base B por la altura.
Área lateral, área superficial y volumen de un cilindro o prisma |
|||
|
El área lateral, el área superficial total y el volumen de un cilindro o de un prima están dados por las siguientes fórmulas: |
|||
| Sólido | Área Lateral | Superficie Lateral Total | Volumen |
| L | T | V | |
| Prisma | p.h | ph + 2B | Bh |
| Cilindro | 2¶rh | 2¶r (r+h) | ¶r2h |
| donde p es el perímetro de una de las bases del prisma, h es la altura, r es el radio de una de las bases del cilindro y B es el área de una base. | |||
►Conos:
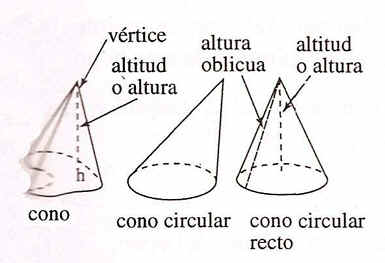
Un cono se forma trazando segmentos desde una figura plana, la base, hasta un punto llamado vértice. El vértice no puede estar en el mismo plano que la base.
La altura es un segmento que parte del vértice y es perpendicular a la base.
Los conos más comunes son el cono circular y el cono circular recto. Ambos tienen como base un círculo.
En un cono circular recto, la altura interseca la base en su centro. La altura oblicua de un cono circular recto es un segmento que va del vértice a un punto de la circunferencia de la base.

Al cortar un cono por diversos planos se obtienen distintas curvas geométricas según este plano corte una o ambas hojas de la superficie de revolución:
Circunferencia, si el plano es paralelo a la base y corta a todas las generatrices.
Elipse si no es paralelo a la base y corta todas las generatrices.
Parábola si es paralelo a una generatriz, pero no corta a las dos superficies de revolución.
Hipérbola si corta a las dos superficies de revolución y es paralelo a una sola generatriz.
El cono es una figura muy popular. Son cónicas las puntas de un alfiler, un lápiz muy puntiagudo, los cuernos de un toro, los minaretes de Santa Sofía, y se llaman «coniferas» a un grupo de plantas que adoptan el aspecto de un cono (abetos, sequoias, etc.).
Su tronco es un cono perfecto. En el diferencial de un automóvil los engranajes tienen forma de tronco de cono y también lo encontramos en las macetas de un jardín, en los feces turcos, en la muela de molino, etc.
► Pirámides:
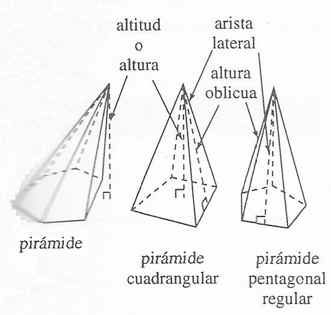
La pirámide es un tipo especial de cono cuya base es un polígono. En la figura se muestra una pirámide típica y algunas de sus partes.
Cada lado de una pirámide es un triángulo denominado cara lateral. Las caras laterales se encuentran en las aristas laterales.
Como en el caso de los prismas, las pirámides se clasifican de acuerdo con la forma de su base. La pirámide regular tiene como base un polígono regular y una altura que es perpendicular a la base en su centro.
La altura oblicua de una pirámide regular es la altura de cualquiera de las caras laterales.
El volumen V de un cono o de una pirámide es un tercio del área de la base B por la altura h, o sea V=1/3Bh. Para las áreas laterales sólo consideraremos las de los conos circulares rectos y de las pirámides regulares.
El área lateral L es la mitad de la altura oblicua s por el perímetro o la circunferencia de la base. El área superficial total es el área lateral más el área de la base.
►La Esfera:
Es un poliedro de infinito número de caras, o bien la superficie engendrada por una circunferencia que gira alrededor de un diámetro.
Las secciones planas o planos que cortan la esfera perpendicularmente a un diámetro dan siempre círculos o circunferencias, según se considere la superficie esférica o la esfera, es decir, el espacio y el volumen abarcado por la primera.
El diámetro generatriz determina dos polos.
El plano perpendicular al centro de la generatriz origina una circunferencia máxima o ecuador.
Si cortamos la superficie esférica por medio de planos paralelos a este ecuador, obtendremos circunferencias cada vez de menor radio hasta que éste será cero.
Entonces el plano se habrá convertido en tangente a la esfera en el punto citado. Todos estos círculos se llaman menores y su radio es tanto menor cuanto mayor sea la distancia del plano al centro de la esfera.
Si dos círculos tienen el mismo radio, su alejamiento del centro de la esfera es el mismo.
Una circunferencia es una línea que determinan 3 puntos, pues solamente por 3 puntos no situados en línea recta puede pasar una circunferencia.
Una esfera necesita 4 puntos no situados en el mismo plano ni 3 de ellos en línea recta para determinar una única esfera.
La condición de estar en un mismo plano no puede aplicarse a una circunferencia porque 3 puntos ya determinan un plano; en cambio, 4 que estén en un mismo plano, no pueden determinar una esfera.
Áreas en la esfera: Prescindimos de las demostraciones, que serían excesivamente largas, y nos limitamos a considerar las siguientes superficies que se pueden originar en la esfera:
Zona esférica es la superficie comprendida entre dos planos paralelos, sea este un círculo máximo o no. Su área es igual al producto de una circunferencia máxima por la altura de la zona: (ver figura abajo)
Área zona esférica = 2.¶.R.h
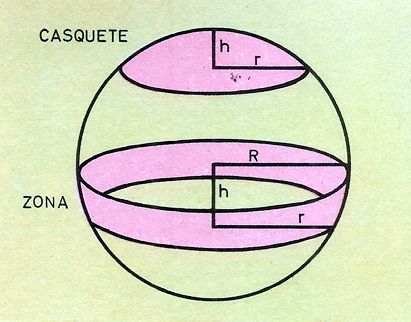
h: es la distancia entre circunferencias del casquete o la altura del casquete
R: radio de la circunferencia máxima
Esta fórmula es igual que la obtenida para el cilindro, es decir, el área de una zona esférica es igual que la de un cilindro de base igual al círculo máximo de la zona, y de altura idéntica a la misma.
Casquete esférico es una zona cuya base superior es un punto. Por tanto, su área vale igual que la de una zona: 2.¶.r.h
r: radio del casquete
Área de la superficie esférica. Es el área total de la esfera es: A= 4.¶.R²
► El Planeta Tierra, Casi Un Esfera
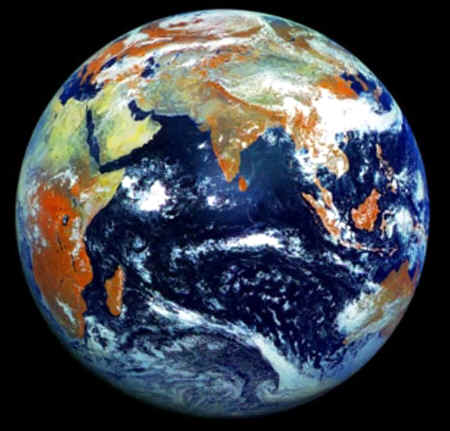
LA ESFERA QUE HABITAMOS: Nuestro planeta Tierra no es exactamente una esfera pues el radio ecuatorial es algo mayor que el polar. El primero mide 6.378.388 m, y el segundo 6.356.912 m.
El achatamiento es de unos 21 km, cifra insignificante si se tiene en cuenta que el ecuador mide 40.076.594 m.
Conociendo el radio es fácil calcular la superficie terrestre, que es de 510.101.934 km2. El volumen de nuestra esfera alcanza una cifra impresionante: 1.083.319.780.000 km3. Se calcula, aproximadamente, que el peso tota! de la Tierra es superior a 5.977 trillones de toneladas.

NOMBRE DE LOS CUERPOS GEOMÉTRICOS

FORMULA VOLUMEN CUERPO: CUBO
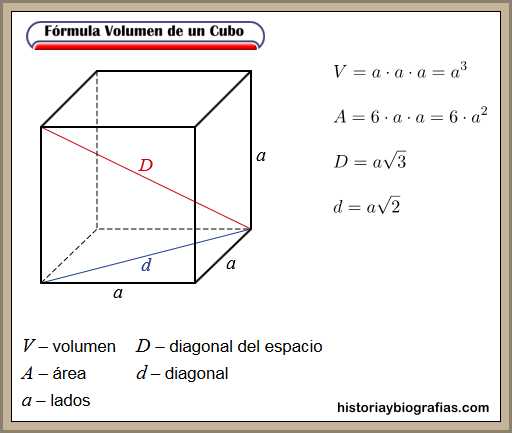
FORMULA VOLUMEN CUERPO:PARALELEPIPEDO
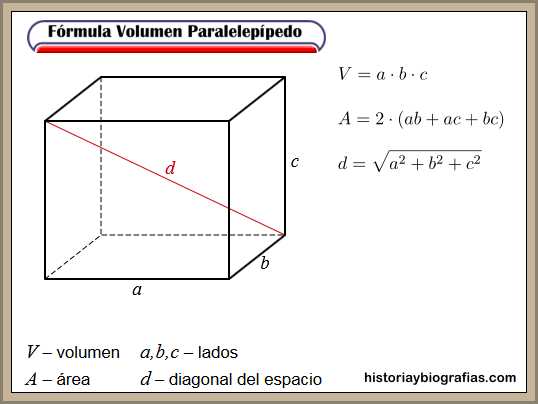
FORMULA VOLUMEN CUERPO:PRISMA

FORMULA VOLUMEN CUERPO:PIRAMIDE
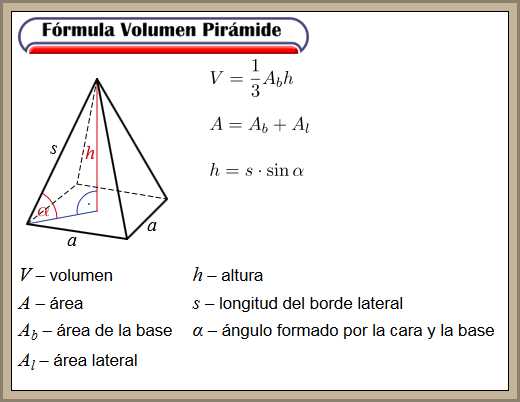
FORMULA VOLUMEN CUERPO:CONO
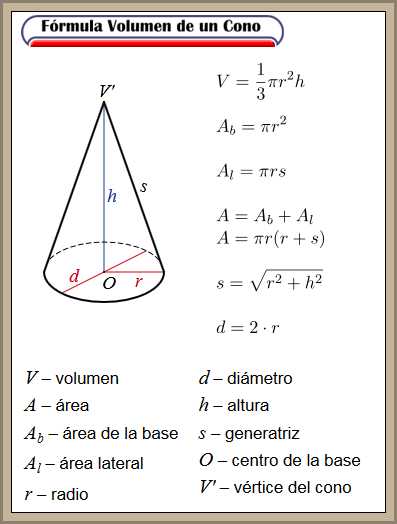
FORMULA VOLUMEN CUERPO:ESFERA
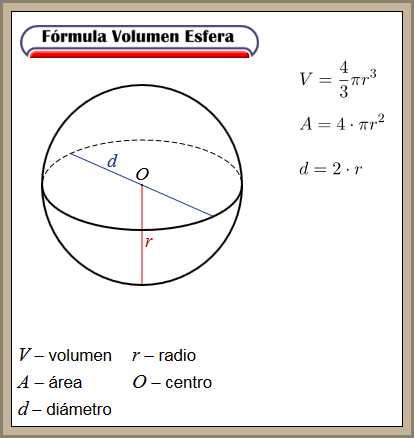
FORMULA VOLUMEN CUERPO:CILINDRO

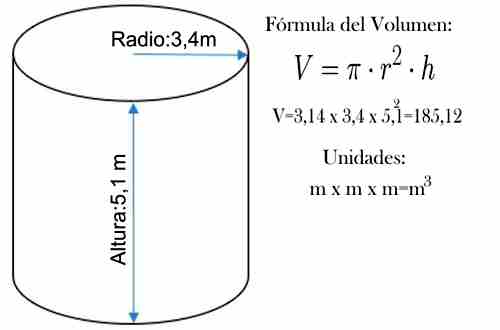
Veamos un ejemplo:
Calcular el volumen de un tanque de base circular cuyo radio es de 3,4 m. y su altura es de 1,2m....Si la base es circular, sabemos que es un cilindro, por lo tanto el calculo se reduce a buscar la fórmula del volumen de un cilindro, que es la siguiente:
Temas Relacionados:
Duplicar el volumen de un cubo Problema de la Antiguedad
Medidas y Unidades Antiguas de Longitud,Superficie y Volumen
Calcular La Densidad de Un Solido:Metodo Practico y Simple
Curiosidad: Geometria Panal de Abejas Celda Hexagonal de los Panales
Enlace Externo:• Cómo calcular el volumen de las figuras geométricas