La Dilatacion Termica de los Materiales:Teoria,Formulas y Aplicaciones
La Dilatacion Termica de los Materiales:Teoria,Formulas y Aplicaciones
Los efectos comunes de cambios de temperatura son cambios de tamaño y cambios de estado de los materiales.
Consideremos los cambios de tamaño que ocurren sin cambios de estado.
Tomaremos como ejemplo un modelo simple de un sólido cristalino. Los átomos están sostenidos entre sí, en un ordenamiento regular, mediante fuerzas de origen eléctrico.
Las fuerzas entre los átomos son similares a las que ejercería un conjunto de resortes que unieran los átomos, de manera que podemos imaginar al cuerpo sólido como un colchón de muelles.
Casi todos los sólidos se dilatan cuando se calientan, e inversamente se encogen al enfriarse. Esta dilatación o contracción es pequeña, pero sus consecuencias son importantes.
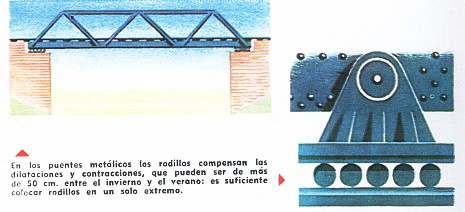
Un puente de metal de 50 m. de largo que pase de 0° a 50 podrá aumentar unos 12 cm. de longitud; si sus extremos son fijos se engendrarán tensiones sumamente peligrosas.
Por eso se suele montarlos sobre rodillos como muestra la ilustración.
En las vías del ferrocarril se procura dejar un espacio entre los rieles por la misma razón; este intersticio es el causante del traqueteo de los vagones.
Mas abajo se muestra una tabla de dilatación de algunas sustancias. Conocido el coeficiente de dilatación es necesario multiplicarlo por el número de centímetros y por el número de grados, para saber cuál será la extensión total del sólido en las condiciones que deberá soportar.
En otras palabras, si el sólido tiene 1,50 m. y la variación de temperatura es de 30° habrá que multiplicar ese coeficiente tan pequeño por 150 y por 30 a fin de conocer su dilatación total en centímetros.
Coeficientes de dilatación lineal
(por cada grado de temperatura y centímetro de longitud)
Aluminio 0,000024
Bronce 0,000018
Hormigón 0,000018
Cobre 0,000017
Fundición de hierro 0,000012
Acero 0,000013
Platino 0,000009
Vidrio térmico 0,000003
Vidrio comercial 0 000011
Cuarzo fundido 0,0000005
Invar (aleación) 0,0000009
Roble, a lo largo de fibra 0,000005
Roble, a lo ancho de fibra 0,000054
Caucho duro 0,000080
► ¿POR QUÉ SE DILATAN LAS SUSTANCIAS CON LA TEMPERATURA?
La temperatura no es más que la expresión del grado de agitación de las partículas o moléculas de una sustancia. Cuando se da calor a un sólido se está dando energía a sus moléculas; éstas, estimuladas, vibran más enérgicamente.
Es cierto que no varían de volumen; pero se labran un espacio más grande para su mayor oscilación, de manera que al aumentar la distancia entre molécula y molécula el sólido concluye por dilatarse.
La fuerza que se ejerce en estos casos es enorme.
► ALGUNAS APLICACIONES
La dilatación térmica puede aprovecharse. El aluminio, por ejemplo, se dilata dos veces más que el hierro.
Si soldamos en una barra dos tiras paralelas de estos metales y la calentamos, la mayor dilatación del aluminio hará que la barra se doble hacia un lado; y si la enfriamos ocurrirá exactamente al contrario.
Habremos fabricado así un termómetro que puede señalarnos las temperaturas y, en ciertos casos, un termostato, como muestra la ilustración.
La dilatación tiene aplicaciones industriales.
El cilindro debe ajustar perfectamente en su camisa. P
ara colocarlo se lo enfría en oxígeno líquido; se lo coloca mientras está contraído, y al dilatarse y recuperar la temperatura ambiente queda firmemente sujeto en su lugar.
Existen así muchos disyuntores, que cortan la corriente eléctrica, o aparatos que desencadenan algún otro proceso, cuando la temperatura llega a un punto crítico.
► MEDIDA DE LA DILATACIÓN
En la figura se ilustra el aparato que se utiliza para determinar la dilatación lineal. En esencia consiste en calentar una barra de longitud conocida hasta una temperatura determinada y medir cuánto se ha dilatado.
La dilatación superficial será el doble de la lineal y la dilatación en volumen el triple de ésta.
La razón es muy sencilla: si el cuerpo tiene longitud uno, y llamamos a la dilatación “d", la longitud dilatada será l + d; la superficie una vez dilatada será 1 + 2d + d², pero d² es tan pequeño que no se tiene en cuenta; y lo mismo ocurrirá para el volumen, cuya fórmula es l+3d+3d²+d3, puesto que los dos últimos términos son tan pequeños que tampoco se los tiene en cuenta.
Conviene recordar esta eliminación de cantidades inapreciables para muchas otras aplicaciones, como el cálculo de errores.


► ALGUNAS RESPUESTAS
• En las carreteras de hormigón o en los embaldosados de gran tamaño se ven, a intervalos regulares líneas de material asfáltíco destinadas a absorber las dilataciones producidas por el calor; de otro modo la construcción saltaría en pedazos en los días de mucho sol.
• El vidrio común es un mal conductor del calor y se dilata apreciablemente; si echamos agua hirviendo en un vaso grueso, la parte interior se calienta y expande, mientras la parte exterior queda fría y encogida, de modo que el recipiente se rompe. Si previamente, colocamos una cucharilla capaz de absorber el calor, neutralizaremos en parte la brusquedad del ataque y, posiblemente, salvaremos el vaso.
• El vidrio pirex se usa para cambios bruscos de tempetatura, simplemente porque su coeficiente (le dilatación es muy bajo y se libra así del peligro de ruptura.
• Los líquidos se dilatan mas que los sólidos: el mercurio sube en el termómetro porque se dilata más que el recipiente de vidrio que lo contiene.
• Los gases, cuyas moléculas son más libres, tienden a dilatarse más que los líquidos.
• Cuando se necesita unir vidrio con metal, como en los tubos de vacío, se usa el kovar que, además de hierro, contiene 29 % de níquel y 17 % de cobalto y su dilatación es idéntica a la del vidrio.
• La aleación invar, que además del hierro contiene 36 % de níquel y 0,15 % de carbono, es prácticamente insensible a los cambios de temperatura; se la emplea en trabajos de geodesia, en péndulos de compensación, en relojes de gran precisión, en patrones de longitud y en muchos instrumentos de medida.
• Hay una serie llamada ni-span que contiene níquel y titanio. Una de ellas se dilata muy poco, como el invar; otra variedad se dilata muchísimo; y la tercera mantiene su módulo de elasticidad (es sabido que el calor afecta mucho la resistencia de los metales) y se la usa, por lo tanto, en resortes para instrumentos de precisión.
• Los proyectiles teledirigidos, que emplean materiales de cerámicas, usan también la aleación kovar.
• La corriente eléctrica calienta los cables o los conductores porque los electrones chocan contra las moléculas, las agitan y la temperatura no es más que el grado de actividad de dichas moléculas.
• Para transportar grandes cantidades de electricidad desde las centrales se usa alto voltaje con el fin de bajar la intensidad, porque es la cantidad de electrones la que provoca el mayor calor y no el voltaje que se aplica.
• La fricción calienta porque tiende a desplazar las partículas que rozan y éstas reaccionan vibrando.
Los campos magnéticos oscilantes que cambian miles o millones de veces por segundo de orientación, provocan cambios en la dirección de las órbitas de los átomos y concluyen provocando una agitación interna que se manifiesta por una mayor temperatura.
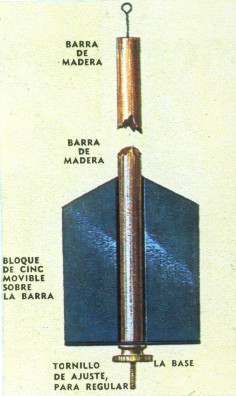
El período de oscilación de un péndulo varía con su longitud; entonces se procura que ésta sea invariable utilizando materiales cuyas respectivas dilataciones se contrapesan.
En la ilustración el equilibrio se obtiene así: el cinc, que proporcionalmente se expande más, es más corto que la borro de modero, menos variable.
En definitivo, los dos dilataciones opuestos se anulan y la oscilación del péndulo es uniforme, o pesar de los cambios de temperatura o que puedo estor expuesto.
------------- 00000 ------------
FORMULAS:EXPLICACION FISICA MATEMATICA
Como decíamoa antes ls efectos comunes de cambios de temperatura son cambios de tamaño y cambios de estado de los materiales.
Consideremos ahora un caso en que el calor solo crea un cambio de tamaño sin llegar a cambio de estado.
Tomaremos como ejemplo un modelo simple de un sólido cristalino.
Los átomos están sostenidos entre sí, en un ordenamiento regular, mediante fuerzas de origen eléctrico.
Las fuerzas entre los átomos son similares a las que ejercería un conjunto de resortes que unieran los átomos, de manera que podemos imaginar al cuerpo sólido como un colchón de muelles.
Estos "resortes” son muy rígidos , y hay aproximadamente 1022 resortes por cada centímetro cúbico.
A una temperatura cualquiera, los átomos de los sólidos están vibrando. La amplitud de vibración es del orden de 10-9cm y la frecuencia aproximadamente de 1013/seg.
Cuando aumenta la temperatura se incrementa la distancia media entre los átomos.
Esto conduce a una dilatación de todo el cuerpo sólido conforme se eleva la temperatura.
El cambio de cualquiera de las dimensiones lineales del sólido, tales como su longitud, ancho espesor, se llama dilatación lineal.
Si la longitud de esta dimension lineal es L, el cambio de longitud, producido por un cambio de temperatura DT, es Al.
Llamamos DT, al salto de temperatura, por ejemplo de 20ºC a 65ºC, entonces el DT=45ºC, puede ser tambien negativo, es decir se enfria salta por ejemplo de 22ºC a 5ºC, entonces DT=-17ºC.
Experimentalmente encontramos que, si DT suficientemente pequeña, este cambio de longitud Al es proporcional al cambio de temperatura DT y a la longitud original L.
Por con siguiente, podemos escribir:(D=delta, letra griega)
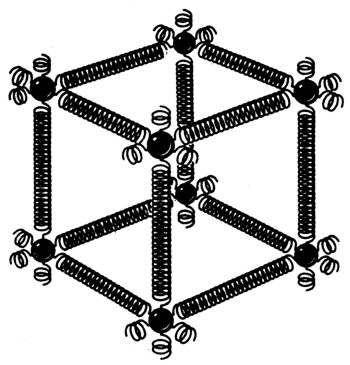
Un sólido se comporta de muchos aspectos como si fuera un "colchón de muelles» microscópico, en el las moléculas están sostenidas entre si mediante fuerzas elásticas
AD [email protected] (se lee alfa L por delta T)
en la ecuación anterior, «, que se llama coeficiente de dilatación U tiene diferentes valores para diversos materiales. Escribiendo otra manera esta fórmula obtenemos:
@= 1.DT/L.DT
o sea, que podemos interpretar a como la fracción de cambio de longitud por cada grado que varia la temperatura.
Estrictamente hablando, el valor de @ depende de la temperatura a que esté el cuerpo y de la temperatura de referencia que se para determinar a L.
Sin embargo, su van ordinariamente es insignificante comparada con la exactitud con es necesario hacer las mediciones en ingeniería.
Con toda confianza podemos tomarla como constante para un material dado, independientemente de la temperatura.
En la Tabla se muestra una lista de los valores experimentales del coeficiente medio de dilatación lineal de algunos sólidos comunes.
Para todas las sustancias se encuentran en la lista, el cambio de tamaño consiste en una dilatación al elevarse la temperatura, porque a es positivo.
El orden de magnitud de la dilatación es aproximadamente de 1 milímetro por metro de longitud por 100 modulos Celsius.
EJjemplo: Se va a elaborar el rayado de una escala métrica de acero de manera que los intervalos de milímetro sean exactos dentro de un margen de precisión de 5x10-5mm. a una cierta temperatura.
¿Cuál es la máxima variación de temperatura permisible durante el rayado?
Tenemos: 5 x 10-5 mm = (11 x 10-6/C)(1.0 mm) DT
en la expresión anterior hemos usado @ para el acero, tomada de la Tabla. De esta expresión se obtiene DT=5 C°.
La misma temperatura a la cual se haga el proceso de rayado será la temperatura a la cual deba conservarse la escala cuando se use y deberá mantenerse siempre dentro de un margen de aproximadamente 5 C°.
Nótese (tabla) que si se usara la aleación invar en lugar del acero, entonces, para la misma tolerancia requerida, se podría permitir una variación de temperatura de aproximadamente 75 C° o para la misma variación de temperatura (DT = 5°), la tolerancia que se obtendría sería más de un orden de magnitud mejor.
TABLA ALGUNOS VALORES DE @
Aluminio 23 x 10-6 Goma dura 80 x 10-6
Latón 19 x 10-6 Hielo 51x10-6
Cobre 17x 10-6 Invar 0.7 x 10-6
Vidrio (ordinario) 9 x 10-6 Plomo 29 x 10-6
Vidrio (pyrex) 3.2 x 10-6 Acero 11 x 10-6
Al nivel microscópico la dilatación térmica de un sólido sugiere un aumento en la separación media entre los átomos en el sólido.
La curva de energía Potencial para dos átomos adyacentes en un sólido cristalino en función de su separación internuclear es una curva asimétrica como la de figura.
Al acercarse los átomos, disminuyendo su separación del valor de equilibrio entran en juego intensas fuerzas de repulsión y la curva de potencial se eleva con gran pendiente (F — dU/dr); conforme los átomos se separan aumentando su separación con respecto al valor de equilibrio.
Fuente Consultada: Tecnirama-Resnik Holliday Tomo I - Wikipedia
Temas Relacionados:
Primeros Descubrimientos Sobre el Calor Historia de los Estudios
Calor Producido Por la Corriente Electrica Aplicaciones
Cantidad de Calor:Concepto de Caloria, Equivalente Mecanico de
Thompson, Conde de Rumford Vida y Obra Científica Sobre el Calor
Los Termometros:Principio de Funcionamiento, Tipos y Errores
Uso de las Fuerzas Naturales:Aplicaciones del Viento, Calor y Agua
Enlace Externo:• Efecto de la dilatación térmica en vías de tren





