Resolucion Ecuacion de Segundo Grado,Aplicando la Resolvente
RESOLUCIÓN ECUACIONES DE 2º GRADO
CALCULO DE LAS RAÍCES EN ECUACIONES CUADRÁTICAS
Por Silvia Ele Profesora de Matemáticas
RESOLVER UNA ECUACIÓN DE SEGUNDO GRADO CON UNA INCÓGNITA:1ra. Parte
Una ecuación de segundo grado es aquella en la cual la incógnita
(generalmente simbolizada por x ) aparece elevada a la segunda potencia.
En general, puede simbolizarse como
![]()
donde 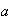 representa al coeficiente del término cuadrático, y nunca puede
representa al coeficiente del término cuadrático, y nunca puede
ser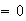 , pero sí puede ser igual a cualquier otro número real.
, pero sí puede ser igual a cualquier otro número real.
 es el coeficiente del término lineal, es decir aquel en que
es el coeficiente del término lineal, es decir aquel en que 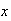 aparece elevada
aparece elevada
a la primera potencia. Puede o no ser igual a 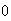 . Y
. Y
 es el término independiente, pues es el coeficiente del término donde
es el término independiente, pues es el coeficiente del término donde
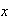 aparece elevada a la potencia
aparece elevada a la potencia 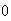 , o sea,
, o sea, 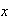 no aparece porque
no aparece porque 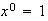 .
.
Según los valores de 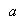 ,
, 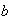 y
y 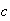 , las ecuaciones de segundo grado se clasifican en
, las ecuaciones de segundo grado se clasifican en
1.Completas, cuando 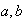 y
y 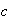 son distintas de
son distintas de 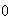 .
.
2.Incompletas, cuando
2.1 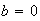 , o sea, no contiene término lineal,
, o sea, no contiene término lineal,
o bien  cuando 2.2
cuando 2.2 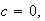 es decir, no existe término independiente.
es decir, no existe término independiente.
Veamos 2.1. La forma general sería

En este caso, la resolución es fácil:

 de donde
de donde 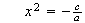
Por lo tanto

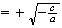 y
y 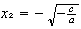
Por ejemplo:
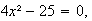
se resuelve así: 
de 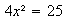 , es
, es 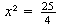 , y
, y 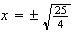
Por lo tanto, 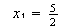
 y
y 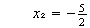
2.2Si 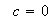 , es
, es 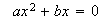
En este caso, para resolver, extraemos el factor común, y nos queda

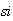
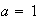
Que es lo mismo que 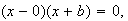
y este producto dará 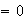 sólo si
sólo si 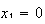 , (porque el primer factor será
, (porque el primer factor será 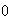 ,
,
y multiplicado por lo que sea que valga el otro, dará producto 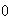 ), o bien si
), o bien si
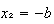 (ya que
(ya que 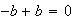 ).
).
Por ejemplo, 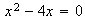 se puede pensar como
se puede pensar como
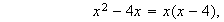 o sea
o sea 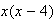
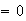 , que tendrá
, que tendrá
como raíces 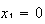 y
y 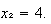
Volviendo al caso general, si 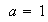 , se dice que las ecuaciones son Reducidas.
, se dice que las ecuaciones son Reducidas.
Veamos cómo se resuelve una de estas joyitas cuando 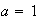 , y
, y 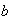 y
y 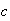 son
son
distintas de 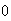 .
.
Su forma sería 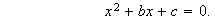
Pensémoslo en un ejemplo: 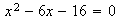 .
.
Si hacemos un conveniente pasaje de miembro ( el viejo truco ),
nos queda 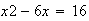 [1]
[1]
Si observamos el primer miembro, vemos que podría corresponder a los dos
primeros términos de un trinomio cuadrado perfecto ( o sea, el cuadrado de un
binomio), donde
 es el cuadrado del primer término del binomio,
es el cuadrado del primer término del binomio,
 sería el doble producto del primero por el segundo,
sería el doble producto del primero por el segundo,
pero nos faltaría el cuadrado del segundo.
Ahora bien, si 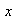 es el primer término del binomio,
es el primer término del binomio, 
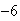 sería el producto de
sería el producto de 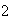 (doble producto, dijimos) por el segundo.
(doble producto, dijimos) por el segundo.
Si llamamos 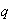 al segundo, donde
al segundo, donde
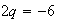 implica que
implica que 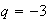 .
.
Y el binomio sería 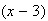
Entonces, apelando al otro viejo truco: "sumo y resto lo mismo y no altero
la suma", puedo escribir
 (porque
(porque 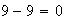 )
)
Y, asociando convenientemente, queda
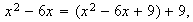
o sea, 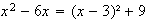
Entonces, reemplazando en [1], queda 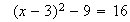
y, resolviendo, será
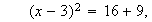
y
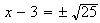
o sea  de donde
de donde 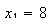
y 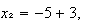
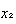
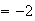
Generalizando lo anterior, se ve que este mismo proceder es aplicable a
cualquier ecuación general de 2º grado con una incógnita. O sea, si:
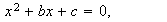
será 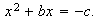
Y si utilizamos el recurso del trinomio cuadrado perfecto, veremos que
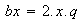 .
.
Entonces, es 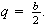
y, si sumamos y restamos  en ambos miembros (nuestro querido y
en ambos miembros (nuestro querido y
viejo truco), será 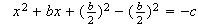
Luego, antes de caer en el colpaso cerebral, hacemos el conveniente
pasaje de miembro y el factoreo del trinomio, y nos quedará
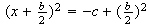
De donde, 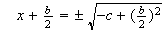
y
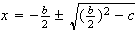 ;
; 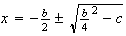 ;
; 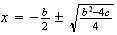 ;
;
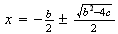 ;
; 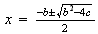
que es lo mismo que
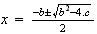 .
.
esto es lo mismo que
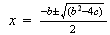
Y si aún queda alguien que desconfíe de este razonamiento, veamos si,
aplicando esta fórmula en la ecuación anterior, llegamos a las mismas
raíces. (Atención: un ejemplo no es una demostración válida, pero si el ejemplo
no coincide con la conclusión, vale para demostrar la no validez de la misma.)
Recordemos que era:
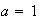 ;
; 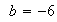 ;
; 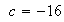
entonces 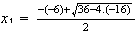
de donde
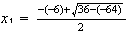 ,
,
pero 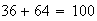 , entonces
, entonces
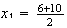 o sea
o sea 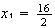 entonces
entonces
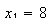 ( que coincide con una de las que hallamos antes)
( que coincide con una de las que hallamos antes)
y
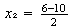 entonces
entonces 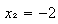 (y que también coincide con la otra que hallamos)
(y que también coincide con la otra que hallamos)
APLICACIÓN ONLINE DE LA RESOLVENTE
Una vez aceptado esto, es una buena idea proponernos, para cuando
egresemos de la sala de terapia intensiva para cerebros exhaustos,
preguntarnos si esta fórmula sirve para todos los casos. O sea,
¿sirve tanto para completas como para las incompletas y para las
que no son reducidas?.
También nos queda para después el análisis de la relación entre el
valor y la "realidad" de las raíces, y el signo de la expresión sub-radical
en la fórmula.
Estos desarrollos los dejamos para otro día, cuando la convalescencia
esté avanzada, y nuestras neuronas hayan recuperado su actividad.
Por hoy, les deseo feliz terapia.
Y les digo "¡Hasta el próximo suplicio!"
"Silvia Ele, la autora de esta colaboración, es una profesora de matemática de muchos años, con quien podés comunicarte enviándole un mensaje a [email protected] "
Temas Relacionados
Regla de Ruffini Online Para Hallar Raices de un Polinomio
Historia del Sistema Metrico Decimal
Trisecar un Angulo con Reglas y Compás
Duplicar el volumen de un cubo
Fórmulas de Volumenes de Cuerpos Geométricos
Enlace Externo:• Ecuaciones de segundo grado y bicuadradas






