Cuadrar un circulo con regla y compas Cuadratura del Circulo Problema
Problema de Cuadrar un Círculo con Regla y Compás
Los Tres Problemas Geométricos Más Famosos De La Antigüedad


Problema 1:Duplicación de un Cubo Problema 2: Trisecar un Angulo Problema 3:Cuadrar Un Circulo
Introducción: Clásico problema de los griegos, el de cuadrar un circulo, osea obtener un cuadrado de igual superficie de un circulo:Antes de abordar la historia de la Geometría alejandrina y como complemento a lo dicho en el capítulo anterior, vale la pena de hablar de los tres problemas que más preocuparon a los griegos desde que aquella ciencia empezó a Construirse racionalmente.
Estos tres problemas son: la duplicación del cubo, la trisección del ángulo y la cuadratura del círculo, que los griegos no supieron resolver, ni nosotros tampoco.
La única ventaja que tenemos sobre ellos es la de saber por qué son irresolubles. Como dichos problemas han trastornado a tantas cabezas de aficionados a la Matemática y todavía existe una pintoresca fauna de locos inofensivos que cree haberlos resuelto, conviene precisar lo que quiere decir “resolver un problema” que es, precisamente, lo que no saben los pobres ilusos que se caracterizan tanto por su ignorancia de Matemática actual y de la historia de esta ciencia como la testaruda resistencia pasiva que oponen a todo intento para convencerles de su error.
En primer lugar, decir que un problema es irresoluble no tiene sentido si no se indica con qué medios o instrumentos, porque pudiera ocurrir que un problema que n tiene solución con ciertos recursos, la tenga con otros; y e segundo lugar, hay que distinguir entre la posibilidad y resolubilidad de de un problema: un problema es posible cuando admite una solución, aunque ésta no se pueda obtener por medio de construcciones elementales, de modo que la resolubilidad es un concepto relativo porque, en sentido absoluto, todo problema posible es resoluble.
La resolución de un problema consiste esencialmente en reducirlo a otro ya resuelto, y, por tanto, se debe llegar a uno, considerado como fundamental, cuya solución se supone dada por uno o varios de los postulados que se refieren al uso legítimo de los instrumentos necesarios para ciertas construcciones geométrica que para los griegos eran la regla y el compás: únicos aparatos de su actividad matemática hasta el punto de que no concedían carta de naturaleza científica a las figuras cuya construcción exige instrumentos distintos de aquéllos.
Con la regla se puede construir la recta que pasa por dos puntos, el punto común a dos rectas no paralelas, y, en general, los problemas de primer grado, es decir: los que, expresados en lenguaje analítico, sólo contienen la primera potencia de la incógnita, y si en el problema entran nociones métricas como las de paralelismo, longitudes de segmentos, valores angulares, etc., es irresoluble con la regla; con el compás es posible describir una circunferencia centro y radio dados, o de centro dado y que pase por punto dado, y determinar los puntos comunes a dos circunferencias secantes, y, por último, con la regla y el compás son resolubles muchísimos problemas siempre que su expresión algebraica sólo contenga raíces cuadradas. Modernamente se ha demostrado que la regla y el compás se pueden sustituir por una regla de bordes paralelos; pero esto no lo sabían los griegos ni lo saben tampoco los actuales cultivadores de la Matemática patológica.
3) Cuadratura de un Círculo:
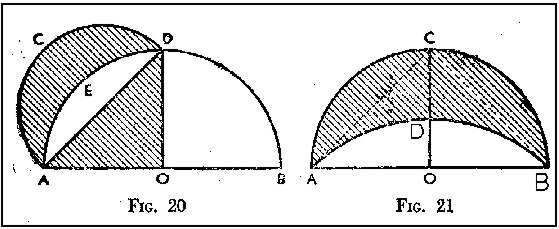
El tercer problema famoso: la cuadratura del círculo, es el más popular de todos y también fue abordado por Hipócrates, quien consiguió cuadrar algunos meniscos ó lúnulas, es decir: figuras limitadas por arcos de circunferencia, como la ACED (fig. 20) y la ACDB (fig. 21), la primera de las cuales, por ejemplo, limitada por el cuadrante AED y la semicircunferencia ACD de diámetro igual a la cuerda de aquél, equivale al triángulo rectángulo AOD formado por dicha cuerda y por los radios OA y OD que pasan por sus extremos, como se demuestra fácilmente. Los descubrimientos de Hipócrates hicieron concebir la esperanza de cuadrar el círculo por sucesivas cuadraturas de lúnulas, y como todos los intentos fueron estériles, se pensó en otros medios que condujeron al descubrimiento de algunas curvas notables, como la concoide de Nicomedes y la cisoide de Diocles, matemáticos ambos de la épocas alejandrina.
Conclusión:
Los problemas de duplicar el cubo y trisecar el ángulo, son problemas irracionales, es decir problemas cuyas soluciones son irracionales, y como dependen de ecuaciones de tercer grado no se pueden resolver con a regla y el compás por exigir construcciones en el espacio. La cuadratura del círculo es de otra naturaleza, pues depende del número PI que no puede ser solución de ninguna ecuación de coeficientes enteros, según demostró Lindemann el año 1882, y, por tanto, dicha cuadratura también es imposible con regla y compás. A pesar de que desde el año 1775 la Academia de Ciencias de París tomó el acuerdo —adoptado después por otras— de rechazar las pretendidas soluciones de estos tres problemas, siguen lloviendo sobre las corporaciones, científicas multitud de comunicaciones acerca de los mismos, que, naturalmente, van a parar al cesto de papeles sin ser leídas, y esto —que ya está divulgado hasta la saciedad de libros y revistas— no ha bastado, ni basta, ni bastará para curar la enfermedad que padecen los duplicadores, trisectores y cuadradores, a los que hay que añadir los “demostradores» del Postulado de Euclides, empeñados en no emplear más armas que las de los griegos antiguos porque ignoran la existencia de las bombas atómicas de la Matemática actual que han demostrado la insuficiencia de los primitivos artefactos bélicos.
Ni qué decir tiene que la ignorancia de los duplicadores, trisectores, cuadradores y postuladores, va unida a una insigne pedantería que les inspira un olímpico desdén por quienes les aconsejan honestamente que se enteren de los trabajos hechos por sus predecesores para soslayar el peligro de descubrir Mediterráneos, porque todos ellos excepción— se creen genios desconocidos, y desde 1uego superiores al medio matemático de su época, y los más enterados se consideran en el caso de un Ruffini, que no con siguió que el Instituto de Francia examinara su demostración de la imposibilidad de resolver por radicales las ecuaciones algebraicas de grado superior al cuarto, o de un Grauss, que no quiso publicar sus investigaciones sobre las Geometrías no-euclídeas por temor al “clamoreo de los beocios”.
El culpable de la imposibilidad de construir un cuadrado y un circulo con el mismo área es el número pi, el famoso 3,1416. Claro que no termina ahí, sino que tiene infinitos decimales. Pi es un número que los matemáticos llaman trascendente, esto es, que no se puede obtener como solución de una ecuación que contenga, además de la consabida incógnita, números positivos, negativos o fracciones -lo que se conoce como números racionales-. Por este motivo, el área de un cuadrado, lado por lado, nunca puede ser igual a la de un círculo, pi por el radio al cuadrado.






