Matematicos de la Edad Media y La Matematica Medieval
Matematicos de la Edad Media y La Matematica Medieval
Respecto a los primeros pasos de la matemática diremos que Pitágoras de Samos, en la Grecia antigua, instauró las matemáticas como ciencia. Pitágoras y su maestro Tales de Mileto son los primeros filósofos de la civilización.
Entonces, se consideraban las matemáticas como una rama de la filosofía, pero hoy día constituye un campo independiente, íntimamente ligado con la lógica.
Los contenidos y conceptos matemáticos se basan en la realidad objetiva. Sin embargo, las matemáticas son abstractas al no estar ligadas a entidades concretas y se basan en axiomas, definiciones y de ducciones lógicas. Por ello, las matemáticas se pueden utilizar en la resolución de problemas concretos.
La aplicación de los números
Las matemáticas nacen con las primeras civilizaciones avanzadas. El estudio sistemático de los cálculos y la geometría se iniciaron allí donde se empezaron a desarrollar el arte, la arquitectura, la escritura, la justicia y la filosofía.
Los negocios y el tráfico comercial no llevaron únicamente bienes materiales a otros pueblos, sino que se produjo una transferencia de conocimientos, experiencias comunes y nuevas percepciones de la vida.
La numeración arábiga, de origen indio, llegó a Europa medieval gracias a los árabes.
Las primeras incursiones en la geometría estaban relacionadas con necesidades prácticas. Por ejemplo, las inundaciones anuales del río Nilo, en Egipto, proporcionaban a los campesinos tierras fértiles pero, al mismo tiempo, hacían desaparecer los límites entre sus campos.
Esto significa que, cada año, debían ser medidos y definidos de nuevo, lo que, evidentemente, requería métodos avanzados. También en la arquitectura se necesitaban cálculos y herramientas geométricas.
Por ejemplo, en la planificación de las estructuras monumentales los arquitectos debían tener en cuenta no solo las fuerzas físicas que Intervenían, sino también las directrices religiosas en cuanto a la orientación de las mismas.
• EN ORIENTE:
Tras la caída del Imperio Romano, la ciencia se decayó en Occidente. Más atento a los logros de los griegos estuvo el mundo islámico, donde se tradujeron muchas obras al árabe, estimulando con ello un pensamiento original en múltiples áreas.
Con la traducción de obras islámicas al latín a partir de 1100 d.C, Europa inició su transformación.
Pese a que el ámbito griego fue el escenario de un florecimiento extraordinario de la filosofía y la ciencia entre 600 y 300 a.C, este no fue un fenómeno que se diera en el vacío: la astronomía y las matemáticas se estudiaban en India, Persia y entre los sábeos del este de Siria.
Tras la caída del Imperio Romano de Occidente en el s. V d.C, la ciencia prácticamente desapareció en sus antiguos dominios, mientras que en Oriente, los sabios, en particular los nestorianos de Siria, fundaron centros de enseñanza de inspiración griega a partir de los cuales se difundieron las ideas griegas en latín, griego, siríaco y persa.
Al mismo tiempo, las ideas viajaban en dirección opuesta desde China, India y Persia, creando un ambiente fecundo para el debate en centros como Bizancio.
Entre 622 y 750 d.C, las tribus árabes unidas por el Islam conquistaron Siria, Persia, Egipto, el norte de África e Hispania.
En este ámbito surgió una fascinación renovada por el saber, y las traducciones de obras filosóficas, matemáticas y científicas griegas fueron la base de la ciencia árabe.
Un importante elemento innovador fue el énfasis de la cultura islámica en la experimentación, en las pruebas empíricas como base de la verdad científica.
En el s. X comenzó una era de investigaciones originales que duró hasta el s. XIII y produjo grandes avances en astronomía,matemáticas y medicica.
En muchas ramas de la ciencia pasaron siglos hasta desarrollar plenamente ideas planteadas ya en el mundo antiguo, occidental y oriental.

AL-JWARIZMI
Pese a que Abu Ya'far Muhammad Ibn Musa al-Jwarizmi fue el matemático, astrónomo y geógrafo persa más destacado de su tiempo, se sabe poco de su vida. Probablemente nació en Jwarizm (Corasmia), en e! actual Uzbekistán, pero pasó la mayor parte de su vida adulta en la Casa de la Sabiduría (biblioteca y centro intelectual) de Bagdad.
Conocido a veces como «padre» del álgebra, estableció esta disciplina como una rama de las matemáticas, difundida después por el mundo occidental a través de las traducciones de sus escritos junto con los números ¡ndoarábigos. El término «álgebra» deriva de al-jabr, parte del título de su libro sobre el tema, Hisab al-jabr wal-muqabala.
EL CÁLCULO
En el s. V d.C, Zu Zhongzhi usó el cálculo para hallar el volumen de una esfera; mil años después, Bonaventura Cavalieri formuló para idéntico fin lo que se conoce como principio de Cavalieri. Pierre de Fermat aplicó el cálculo a las líneas curvas. Muchos años despúes Isaac Newton lo aplicó a la física en general, mientras que su coetáneo Cottfried Leibniz creó gran parte de la notación que se usa en el cálculo.
------------- 00000 ------------
• EN OCCIDENTE:Dos Grandes Matemáticos
 Leonardo de Pisa (Fibonacci)
Leonardo de Pisa (Fibonacci)
1170-1250
LEONARDO FIBONACCI: El pisano Fibonacci aprendió el sistema numérico indoarábigo trabajando con su padre, un mercader establecido en el puerto argelino de Bugía, y luego estudió con matemáticos árabes.
En 1202 publicó el Líber abad, donde explicaba las ventajas del empleo de los dígitos de 0 a 9 y el valor posicional (consistente en que cada dígito aumenta diez veces el valor de su posición a la derecha) para actividades comerciales como llevar los libros de contabilidad.
La obra fue muy influyente en Europa. Entre sus libros posteriores figura Practica geometriae, sobre la geometría y la trigonometría árabes.
LA MATEMÁTICA EN LA EDAD MEDIA:
En su crepúsculo, el siglo v asiste al dramático fin del Imperio Romano de Occidente.
Con la invasión de los bárbaros desciende sobre Europa la milenaria "noche medieval", la larga noche de estancamiento y decadencia de todas las ramas del saber.
Cuando Alejandría sucumbe ante los musulmanes y el emperador JUSTINIANO cierra, en el año 529, las antaño famosas escuelas de Atenas, sólo Constantinopla custodia la preciosa herencia de la cultura antigua.
Hasta la toma de la ciudad por los turcos en 1453, y la consiguiente difusión por Occidente de manuscritos y conocimientos griegos, el mundo queda sumido en densas sombras, cuya penumbra sólo es surcada por la luz que enciende un pueblo extraño a Europa: los árabes.
Las tres centurias que siguen al fin del Imperio de Occidente y que preceden a la aparición de los árabes en escena, son la época más estéril en la Historia de las Ciencias.
Sobre la ruina de las instituciones sociales y políticas del mundo romano se eleva poderosa la nueva organización de la Iglesia; subordinados a sus finalidades, todos los esfuerzos intelectuales convergen en su seno.
En el concepto de los padres de la Iglesia -moralistas eminentes, pero ignorantes en la ciencia como es hoy un niño de diez años- el mundo físico es el escabel de Dios y sus fenómenos parecen menos dignos de estudio que los problemas teológicos, únicos capaces de servir a la salvación de las almas.
El universo para el hombre medieval sólo tiene una extensión de algunos miles de kilómetros; su pasado abarca algunos millares de años y su fin, una amenaza para los pecadores, está muy cercano.
En este pequeño mundo, destinado a pronta e inevitable destrucción, ¿qué sentido, qué utilidad, podrían tener las ciencias?.
La astronomía se reducía a reglas para establecer el calendario de la Iglesia, a algunos preceptos indispensables para los navegantes, o aun a una quimérica doctrina acerca de las influencias astrales sobre los destinos humanos.
Las matemáticas quedan, en el Occidente cristiano, dentro de los límites de la aritmética elemental, seguidas de especulaciones neoplatónicas sobre las propiedades místicas de los números.
Algunas definiciones de triángulos, cuadriláteros, círculos y sólidos constituyen todo el edificio, antaño tan soberbio, de la geometría.
La química se identifica con la búsqueda del oro alquímico o de una panacea universal.
------------- 00000 ------------
COPÉRNICO Y GALILEO: Para que el saber científico pudiese avanzar, en ocasiones era preciso subvertir creencias religiosas erróneas. De sus observaciones, Copérnico dedujo que la Tierra gira alrededor del Sol mientras rota sobre su eje, y Galileo se sumó a la idea tras observar el paso de satélites ante la faz de Júpiter.
------------- 00000 ------------
La Matemática en el Medioevo Europeo
En el continente europeo, la Matemática no tiene un origen tan antiguo como en muchos países del Lejano y Medio Oriente, alcanzando sólo éxitos notorios en la época del medioevo desarrollado y especialmente en el Renacimiento.
En la Edad Media se puede observar cierto oscurantismo cultural, sin duda debido a los acontecimientos bélicos y sociales de la época.
Sólo en algunos monasterios religiosos se escribieron algunos manuscritos, testimonios de un primer despertar cultural.
La Matemática interesa en Europa por el contacto con los árabes. Hasta esa época se conocía la Geometría de los griegos a la que no se le había agregado casi nada, el sistema de numeración decimal, posicional y con cero de los hindúes y generalizado por los árabes, el Álgebra y la Trigonometría de los árabes.
Los números eran los naturales, racionales, irracionales, todos positivos.
Los negativos eran soluciones falsas.
A partir de los siglos XII y XIII, principalmente por el contacto con los árabes, los occidentales comienzan a dar fundamentos, ya visualizados hasta entonces de la Matemática.
El punto de arranque de la Matemática en Europa fue el desarrollo de los Centros de Enseñanza, París en 1200, Oxford en 1214, etc.
Con anterioridad, tan solo algunos monjes se dedicaron a estudiar las obras de Ciencias Naturales y Matemática de los antiguos.
Uno de los primeros centros de enseñanza fue organizado en Reimsgs por Gerberto de Aurillác (940-1003) donde fundamentalmente se hacen traducciones.
Cerberto fue profesor durante 10 años en Reims, luego obispo de esa ciudad y de la de Raveno, y al final de su vida se convirtió en el Papa Silvestre II.
Conoció y propagó la notación decimal que aprendió en España durante su estancia en un convento catalán en 967.
Esto ocurre en el siglo X.
Fue posiblemente el primero en Europa que enseñó el uso de los numerales hindú-arábigos.
Sin embargo hubo que esperar a que los musulmanes rompieran la barrera lingüística, hacia el siglo XII, para que surgiera una oleada de traducciones que pusieran en marcha la maquinaria matemática. Esta época fue caracterizada por las traducciones.
Se comienza a traducir todo. Las obras griegas ya habían sido traducidas al árabe.
Hay que traducir todo del árabe, se traducen en España.
Las traducciones se hacen al latín pasando por el idioma local.
Por ejemplo al español, y de ahí al latín. El trabajo de los traductores fue sensacional y se da entre los siglos XI y XIII.
Uno de los lugares donde esto ocurre es en la Escuela de traductores de Toledo100, durante el reinado de Alfonso X el Sabio.
Entre los traductores de Toledo se destaca Gerardo de Cremonam (1114-1187), que tradujo del árabe más de 80 obras.
Sus trabajos de investigación y traducción permitieron que obras fundamentales de la antigua cultura griega fueran rescatadas del olvido y transmitidas a la Europa medieval a través de España.
A partir de estas versiones, y gracias a las mismas, España transmitió a Europa todos aquellos saberes que cubrían campos como la Geografía, la Astronomía, la Cartografía, la Filosofía, la Teología, la Medicina, la Aritmética, la Astrología o la Botánica, entre otros.
Esta escuela fue el origen y la base del renacer científico y filosófico drías famosas escuelas de Chartresm y, más tarde, de la Sorbona.
Durante el siglo XIII surgió la figura de Leonardo de Pisa (1180 1250) más conocido como Fibonacci.
Otro contemporáneo, aunque no tan excepcionalmente dotado fue Jordano Nemorarius (1225-1260).
quien debemos la primera formulación correcta del problema del plano inclinado.
El profesor parisino Nicole Oresmes (1323-1382) generalizó el concepto de potencia, introduciendo los exponentes fraccionarios, las reglas de realización de las operaciones con ellos y una simbología especial, anticipándose de hecho a la idea de logaritmo.
Cuando se traducen los Elementos de Euclides, la fundamentación axiomática lleva a pensar que lo que él hizo para la Geometría, se podría hacer con los números, surge la idea de fundamentar axiomáticamente a los números naturales.
Ya en el siglo XV, época de las grandes navegaciones, la Trigonometría fue separada de la Astronomía, alzándose como ciencia independiente de la mano de Müller (conocido comoRegiomontano) (1436-1474).
De Signos, símbolos y números: Una pizarra cubierta de expresiones algebraicas se ha convertido en una imagen identificativa de las matemáticas académicas. Aunque las ecuaciones sean largas y complejas, y contengan símbolos poco conocidos, las reglas del álgebra siguen siendo válidas.
------------- 00000 ------------
La Ecuaciones Uno de los Problemas de la Matematica Medieval
Los primeros matemáticos carecían de símbolos para representar expresiones y operaciones matemáticas, lo cual era un obstáculo considerable para el progreso. Con la introducción de los símbolos, el álgebra se desarrolló como una rama de las matemáticas y propició importantes avances en otras de sus áreas.
Los antiguos matemáticos babilonios, egipcios y griegos se las arreglaban para describir y resolver los problemas matemáticos expresados en palatyras y números (el álgebra retórica), pero esto era un proceso engorroso.
HacIa falta un sistema en el que el resultado buscado -esto es, la incógnita- se pudiera expresar en los términos de la información conocida sobre él.
El proceso siguió siendo verbal hasta el s. IX cuando el persa Al-Jwarizmi puso los cimientos de lo que hoy se conoce por álgebra al postular reglas sistemáticas y lógicas para resolver ecuaciones.
Matemáticos posteriores expandieron su obra introduciendo símbolos de operaciones como +, -, e=; la x para representar la incógnita y otras letras para las variables.
La invención de estos signos y símbolos matemáticos específicos simplificó la resolución de problemas e instituyó el álgebra como un campo por derecho propio, igualmente útil para resolver problemas en otras disciplinas como astronomía, física y economía, además de problemas cotidianos.
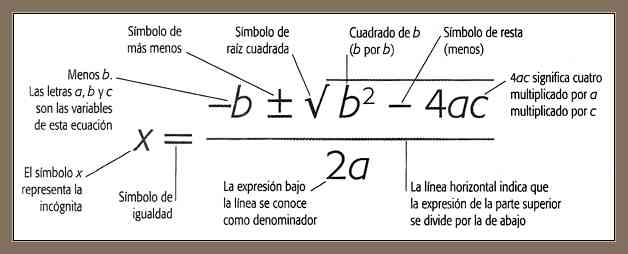
Ecuaciones Algebraicas:
Muchos problemas se pueden expresar en forma algebraica como ecuaciones, y aplicar las reglas del álgebra permite calcular sus incógnitas.
Un ejemplo sencillo sería el siguiente.
Suponga que ha pagado un total de 28,75 $ por artículos de papelería y sabe que dicho precio incluye un 15 % de impuestos. ¿Cuánto costaban los artículos al margen del impuesto?.
Para obtener la solución algebraica, sea la incógnita x.
Luego x más el 15% de a son 28,75 $. En símbolos esto se representa así: x + 0,15x = 28,75 $, o bien 1,15x = 28,75 $. Por tanto, el precio antes de aplicar el impuesto es:
x = 28,75 $ % 1,15 = 25,00 $.
------------- 00000 ------------
El álgebra se puede aplicar también a la resolución de problemas con dos o más incógnitas, como en el ejemplo siguiente.
Van caminando dos burros cargados con pacas de heno.
Uno le dice al otro: -Si me dieras una de tus pacas, los dos llevaríamos el mismo número.
El otro responde: -Si me dieras una de tus pacas, tendría el doble que tú.
¿Cuántas pacas lleva cada uno?.
Para resolver el problema, sea x el número de pacas que lleva el primer burro, e y el número de pacas del segundo.
Entonces, si una paca pasa del burro 2 al burro 1, este tiene x + 1, el burro 2 tiene y - 1, y sabemos que ambos tienen igual número de pacas, por tanto, x + 1 = y - 1. Sumar 1 a cada
lado da x + 2 - y, o y = x + 2.
Por otra parte, si una paca pasa del burro 1 al burro 2, el burro 2 tendrá y + 1 pacas, que es el doble de las que tiene el burro 1 (x- 1).
Dicho de otro modo, y + 1 = 2 (x- 1), o lo que es igual, y + 1 = 2x - 2.
Si se resta 1 de cada lado de la ecuación, queda y - 2x - 3.
Ya sabemos que y = x + 2, así que podemos escribir x + 2 = 2x - 3.
Se resta x de cada lado para que quede 2 = x - 3; luego se añade 3 a cada lado para obtener x = 5, y dado que y = 2x- 3, y = 10 - 3 = 7.
Por lo tanto, la solución es que el burro 1 tenía 5 pacas y el burro 2 tenía 7.
Los mismos principios generales pueden aplicarse a ecuaciones más complejas, pero no siempre se puede resolver explícitamente una ecuación dada.
No obstante, suele ser posible obtener una solución aproximada con un alto grado de precisión.
Temas Relacionados:
Grandes Matematicos Griegos y sus Aportes
Disputas Matemáticas En el Siglo XVI Tartaglia, Cardano y Del Ferro
Los tres problemas geometricos famosos de los griegos
Curiosidades Científicas y Tecnicas De La Historia
Los números perfectos Curiosidades Matematicas
Sólidos Platónicos Poliedros Regulares:Demostración de Pitágoras
Demostración pitagórica del número irracional de la raíz cuadrada






