Biografia de Arquímedes Descubrimientos, Inventos y Obra Científica
Biografía de Arquímedes Matemático y Científico - Obras Científica
► ¿Quien Fue Arquímedes?
Físico y matemático, Arquímedes nació hacia 287 a. C. en Siracusa, en la costa occidental de Sicilia, que entonces pertenecía a Grecia.
Heredó la vocación científica de su padre, quien, al parecer, se dedicaba a la astronomía.
Pasó casi toda su vida en su ciudad natal y murió cuando la isla fue atacada por Roma en -212.
La historia nos cuenta que un día del siglo III a.C, un científico griego que vive en la ciudad siciliana de Siracusa, se encuentra tomando un baño.
Allí se le ocurre la respuesta a un problema que le agobiaba desde hacía tiempo, y sale corriendo desnudo para anunciar su descubrimiento.
Fue Arquímedes el hombre de ciencia que salió de la bañera tal como estaba, para anunciar la respuesta a un problema que le había planteado el rey.
Nacido en Siracusa hacia el año 287 a.C. en el seno de una familia aristocrática, marchó a Alejandría, donde fue discípulo de Euclides, el creador de la geometría.
Al cabo de un tiempo, Arquímedes prefirió volver a su ciudad natal y proseguir sus estudios con total libertad.

BREVE FICHA BIOGRAFICA
• Nació en Siracusa (actual Sicilia, Italia), en el 287 a.C. y se educó en Alejandría.
• Aprendió de su padre varias disciplinas matemáticas.
• Su primera construcción fue la de un tornillo (abajo) que utilizó para extraer agua de los pozos.
• Aseguró que con un punto de apoyo movería la Tierra y para demostrarlo construyó un sistema de poleas con el que puso en movimiento un barco.
Su ingenio impidió que los conquistadores romanos tomaran Siracusa durante tres años. Para detenerlos ideó la catapulta, que permitía arrojar piedras y otros proyectiles y un sistema de espejos con los que incendiaban las naves Jnemigas al enfocarlas con los rayos del Sol.
Realizó numerosos descubrimientos aritméticos y geométricos. Entre ellos, calculó los volúmenes del cono, la esfera y el cilindro y resolvió complicadas operaciones matemáticas.
• Inventó cerca de cuarenta máquinas y artefactos; entre ellos se destacó un sistema de poleas y de planetarios mecánicos, que en su época eran muy populares.
• Murió asesinado por un soldado romano, a los 75 años. Al ser conquistada Siracusa, Arquímedes fue muerto por un soldado romano que le hizo una pregunta cuando estaba tratando de resolver un problema matemático.
En ese momento estaba tan entusiasmado con ese tema, que se molesto al ser interrumpido y ofendió al soldado negándose a abandonar sus cálculos.
Un día, el rey de Siracusa le pidió a Arquímedes que comprobara si una corona que había encargado era realmente de oro.
El matemático pensó y pensó sin saber cómo resolver el problema. Hasta que al darse un baño, observó cómo la bañera se desbordaba, se le ocurrió la solución y gritó; ¡Eureka! ¡Eureka! ("¡Lo encontré! ¡Lo encontré!").
Relacionando el peso de la corona y la cantidad de agua desplazada al sumergirla en agua, comprobó que no era de oro puro.

► Biografía de Arquímedes
Nació en Siracusa en el año 287 a. de J. C. Creció en un ambiente donde la ciencia era familiar, ya que su padre, Fidias, era astrónomo. Arquímedes reveló tempranamente particular disposición para los estudios.
Un científico que dedicó toda su vida al estudio de la física y de las matemáticas, extrayendo aplicaciones útiles.
Además de filósofo y matemático fue un atento observador e investigador del mundo natural.
Sus intereses eran muy variados e hicieron de él uno de los mayores científicos de la Historia.
Supo unir la lógica matemática a la experimentación, por esta razón se le puede considerar un hombre que se adelantó a su tiempo y precursor de Galileo.
De su vida sabemos por ilustres historiadores que no se cansaba jamás de hacer cálculos e inventar.
Con él la mecánica se convirtió en una verdadera ciencia: ya que las máquinas se empezaron a pensar y construir en función de su utilidad.
Viajó por la península ibérica y estudió en Alejandría.
Allí trabó amistad con el famoso Eratóstenes de Cirene, con quien efectuó la medición de la circunferencia terrestre.
Probablemente a consecuencia de los estudios realizados con Eratóstenes, más que por tradición familiar, en Arquímedes nació la afición por la astronomía.
Vuelto a Siracusa, se dedicó a sus estudios de matemática, física, geometría, mecánica, óptica y astronomía.
En todas estas materias realizó investigaciones que aún hoy resultan difíciles para una persona de buena preparación.
El pensamiento científico de Arquímedes era parte integral de su concepción matemática. Revolucionó la mecánica, inventó la hidrostática y fundó el estudio preciso de sólidos más complejos.
Las operaciones que esto requeríale llevaron a inventar una forma primitiva de cálculo diferencial y a una comprensión avanzada de la numerologia. También destacó en la esfera práctica.
Entre sus inventos se cuentan poleas y palancas, una bomba de agua y una forma primitiva del láser.
Es muy probable que hubiera otros de los que no se molestó en dejar constancia de ellos, o que desaparecieron para siempre con sus obras perdidas.
Arquímedes no valoraba sus creaciones prácticas, y pocas veces se molestó en consignarlas.
No obstante, los tratados que sí recogen su obra siguen resultando tan asombrosos y lúcidos como el día en que fueron escritos. Afortunadamente, la mayoría son fáciles de comprender, incluso para los profanos.
Estas obras ofrecen una perspectiva singular sobre el funcionamiento de una mente singular.
Pero incluso una mente como la de Arquímedes no surge de la nada.
Para comprender lo que él comprendió y para apreciar lo que hizo con este saber, es muy importante primero conocer cómo era el mundo antes de que él apareciera en escena.
Imagen Típica del Sabio

ARQUÍMEDES (287 a.C-21 2 a.C): Nació y murió en Siracusa. Fue sin duda el mayor matemático y físico de la antigüedad. Arquímedes, aristócrata en cuerpo y alma, era hijo del astrónomo Feidias. Se dice que era pariente de Hierón II. De todos modos se hallaba en excelentes relaciones con Hierón II y su hijo Gelón, quienes tenían por él gran admiración.
► Inventor infatigable:
Se dice siempre que la ciencia nació en la antigua Grecia y es completamente cierto que en este pequeño rincón del mundo surgieron por primera vez muchas de las ideas que comúnmente definimos como científicas.
Los seres humanos siempre han observado los fenómenos de la Naturaleza, desde los más sencillos como la caída de un objeto, hasta los más complicados e inexplicables.
Pero sólo cuando empezaron a indagar y estudiar planteándose las preguntas adecuadas, nació el método científico que ha permitido progresar en el camino del conocimiento.
Los antiguos griegos se interesaron profundamente por ciencias como la geografía, la biología, la medicina, la astronomía y las matemáticas, además de la filosofía, naturalmente.
A pesar de ello, pocas veces se dieron realizaciones prácticas, es decir, máquinas capaces de ayudar en el trabajo.
En este sentido, Arquímedes fue una excepción.
Todo el mundo ha oído hablar del principio de Arquímedes: "Todo cuerpo sumergido en agua recibe de parte de este líquido un impulso de abajo a arriba igual al peso del volumen de agua que desaloja."
Aquí radica el fundamento de la hidrostática y sus aplicaciones han sido innumerables.
Al salir Arquímedes del baño portador de las dos coronas de oro y plata que le habían servido para su experimento, muy bien podía recorrer las calles de Siracusa gritando "¡Eureka!". Aquel día había efectuado realmente un gran descubrimiento.
Arquímedes en la Bañera

Típica Ilustración de Arquímedes en la famosa bañera donde floreció su
brillante idea del principio que lleva su nombre
Arquímedes no sólo redactó su famoso Tratado de los cuerpos flotantes, sino que también inventó el tornillo sinfín y los engranajes multiplicadores y de multiplicadores, y generalizó la teoría de la palanca.
Nadie ignora esta famosa frase: "¡Dadme un punto de apoyo y levantaré el mundo!" Arquímedes fue igualmente un gran ingeniero.
Cuando el ataque a Siracusa por la flota romana, hizo construir múltiples ingenios destinados a defender la ciudad: ballestas y catapultas que lanzaban flechas y piedras, grúas gigantescas que lanzando un garfio por entre los aparejos de las trirremes, atraían a éstas hacia las rocas contra las que se estrellaban.
El resto de la flota romana fue incendiado por inmensos espejos parabólicos de bronce, prolijamente pulidos, que concentraban a distancia los rayos del sol siciliano sobre las galeras enemigas.
LEGADO LUEGO DE SU MUERTE:
En el momento de la muerte de Arquímedes, la Magna Grecia caía en manos del Imperio Romano.
A mediados del siglo siguiente, Roma había dominado la propia Grecia, y la gran era de la cultura griega antigua llegó a su fin.
El Imperio Romano consideraba el pensamiento griego como un mero ornamento. No cumplía ninguna finalidad práctica.
El genio romano se manifestaba en la ingeniería, el ordenamiento civil y el militarismo.
Su contribución a la matemática sigue siendo una laguna.
El único romano que jugó un papel en la historia de las matemáticas fue el soldado que mató a Arquímedes.
La influencia de Arquímedes en las generaciones siguientes fue mínima.
Sencillamente se pasó por alto la enormidad de sus logros.
Aunque sus fórmulas, como por ejemplo las del área de la superficie y el volumen de la esfera, se convirtieron en parte del canon matemático establecido.
Igualmente también se adoptó su aproximación fácilmente inteligible de n como 22/7 que se aproximaba tres décimas al valor correcto, más que suficiente para los romanos.
Aunque Arquímedes había esperado que su "método mecánico" (que implicaba operaciones exhaustivas, límites y demás) conduciría a nuevos descubrimientos matemáticos.
No sería así.
Sólo cuando las obras de Arquímedes se tradujeron al árabe durante el siglo VIII sus esperanzas empezaron a hacerse realidad.
Mientras que Europa languidecía en las tinieblas, fueron los árabes quienes hicieron arrancar de nuevo a las matemáticas, que habían permanecido en hibernación durante un milenio.
Así fue como las obras de Arquímedes sobrevivieron de una u otra forma durante la Edad Media y posteriormente.
Sus ideas prácticas no parecían contradecir la ortodoxia aristotélica, con lo cual eran aceptables para la mentalidad medieval.
¿Pero qué uso dio a las obras de Arquímedes la mentalidad medieval?.
Casi ninguno, se diría. En Europa las matemáticas siguieron adormecidas.
¿O no? Cierto número de estudiosos sigue convencido de que en algún lugar de Europa alguien tuvo que estimar las obras de Arquímedes por su valor real, y haberse sentido inspirado para continuarlas.
Las matemáticas no requieren tradición social alguna, pueden ser practicadas con la misma facilidad por un monje solitario en una apartada comunidad isleña que por un estudioso en una universidad o un sabio cortesano.
Lo único que habría hecho falta eran las obras de Arquímedes, y alguien con inteligencia suficiente para emplear su método.
Un sólo genio sin ayuda podría fácilmente haber hecho avanzar las matemáticas él solo (y quizá hubiese podido transmitir sus obras, ahorrándole a la civilización siglos de estancamiento intelectual).
Sin embargo, no se han hallado indicios de la existencia de ese genio perdido.
En general, las matemáticas siguieron siendo útiles sólo como herramienta práctica.
La facultad humana para el pensamiento matemático abstracto siguió sin explorarse, salvo quizá para calcular la cantidad de ángeles que cabe en la cabeza de un alfiler.
El impulso hacia la abstracción se vio desviado hacia la estéril especulación teológica.
Esta situación apenas cambió hasta la llegada del Renacimiento.
Hasta mediados del siglo XVI Arquímedes no inspiró a los grandes espíritus tales como Kepler y Galileo.
Aún así, habría de pasar un siglo hasta que Newton hiciera progresos respecto del método de Arquímedes y crease el cálculo.
Cuando le preguntaron cómo había realizado sus grandes descubrimientos, la célebre respuesta de Newton fue: "Si yo he visto más lejos sólo ha sido porque me aupé a los hombros de gigantes".
Pero tanta modestia era sólo aparente. Newton era plenamente consciente de ser un gigante, incluso entre gigantes.
Y el único gigante al que reconocía como su igual era Arquímedes.
► SU OBRA CIENTIFICA:

Luego de varios viajes, cuando regresó a Siracusa, sorprendió a todos con un método de su invención, destinado a desecar pantanos mediante la utilización de diques móviles.
El mecanismo sería conocido como «tornillo de Arquímedes».
Consistía en un tubo en forma de hélice, uno de cuyos extremos quedaba sumergido. Al girar sobre su eje en posición inclinada, servía para elevar el agua.
Los inventos de Arquímedes y su aplicación a máquinas de artillería contribuye ron notablemente a la defensa de Siracusa contra el asedio de los romanos; en este sentido, ideó catapultas de gran potencia y propuso un mecanismo eficaz para provocar incendios —que seria utilizado para destruir parte de la flota enemiga—, mediante el empleo de espejos parabólicos.
El año 212 a. C, Siracusa fue finalmente invadida por las tropas romanas; Arquímedes falleció, atravesado por la lanza de un soldado, en su propia casa.
El rey Marcelo, que admiraba al anciano sabio, y que había ordenado que su vida fuera respetada, hizo elevar un monumento funerario en su honor.
En él aparecía una esfera inscrita en un cilindro, tal y como Arquímedes había deseado.
Su aportación a las matemáticas:
Las investigaciones de Arquímedes en el ámbito de las matemáticas se centraren sobre todo, en la geometría y la aritmética y en lo que hoy se conoce como cálculo integral.
Dentro del campo de la aritmética, escribió dos textos fundamentales. Sobre medida del circulo y El arenarlo.
En la primera de estas obras, uno de sus escritos mi importantes, afirma que la razón entre la circunferencia y su diámetro es igual al sea cual sea el radio de la figura.
Por otro lado, demuestra la equivalencia entre el área del círculo y la de un triángulo rectángulo cuyos catetos son el radio y la longitud de la circunferencia.
En El Arenario Arquímedes propone un método para escribir números de gran longitud, dotando a cada cifra de un orden diferente según su posición.
Entre sus publicaciones sobre geometría, las más representativas son De la esfera y del cilindro, donde introduce el concepto de concavidad, así como ciertos postulados referentes a la línea recta; conoides y esferoides, que contiene la definió de las figuras engendradas por la rotación de distintas secciones planas de un cono y De de las espirales, centrada en el estudio de estas curvas y sus propiedades.
La denominada «espiral de Arquímedes» es resultado del movimiento que describe un punto que se desplaza con movimiento uniforme sobre una recta que gira alrededor de uno de sus puntos; su radio vector es proporcional al ángulo.
Entre las obras que han sobrevivido existe una pequeña obra maestra titulada Mediciones del círculo, que contiene uno de sus mejores ejemplos de argumentación geométrica, aquella en la que explica la relación entre la circunferencia de un círculo y su diámetro, lo cual le permitió obtener un cálculo notablemente preciso del valor de Pi.
El método que utilizó aquí despejó el camino hacia uno de los principales descubrimientos matemáticos.
Arquímedes calculó el área de un círculo descubriendo los límites entre los cuales se hallaba dicha área, y luego estrechando gradualmente esos límites hasta aproximarse al área real.
Esto lo hizo inscribiendo en el interior del círculo un polígono regular y circunscribiendo después el círculo en un polígono similar.
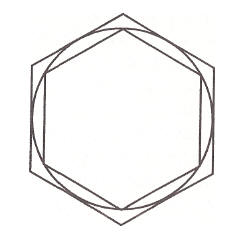
Arquímedes comenzó con dos hexágonos. Doblando el número de lados y repitiendo el proceso obtuvo finalmente polígonos de 96 lados.
Calculó el área del polígono interior, que proporcionaba el límite inferior del área del círculo.
A continuación calculó el área del polígono exterior, la cual proporcionaba el límite superior.
Con este método pudo calcular que: 3 10/71< Pi <3 1/7
En decimales esto da la siguiente ecuación: 3.14084 < Pi < 3.142858
La precisión de este cálculo puede apreciarse por su proximidad a la cifra que hoy manejamos: Pi = 3.1415927.
Aquí la principal innovación de Arquímedes fue emplear la aproximación en vez de la igualdad exacta. Euclides había indicado la posibilidad de emplear este método, pero ni lo aplicó a conciencia ni vio sus posibilidades.
Arquímedes vio que a menudo bastaba con dar dos aproximaciones relativamente fáciles a una respuesta, que proporcionaban un límite superior e inferior entre los cuales se hallaba dicha respuesta.
• Física:
Las aportaciones más importantes de Arquímedes a la física son las relativas a la hidrostática y el equilibrio de los cuerpos.
Sin duda, sus conocimientos geométricos resultaron fundamentales para determinar el centro de gravedad de los objetos sólidos.
Especial interés revisten la ley fundamental de la palanca enunciada por el sabio, y el descubrimiento de la polea compuesta, basada en la ley anterior, que sería empleada por Arquímedes para mover un enorme barco.
En cierta ocasión, Arquímedes le planteó al rey de Sicilia, Hierón, el reto de mover cualquier peso, por grande que fuera, con la simple condición de contar con un objeto firme en el que poder apoyarse.
De este episodio ha pasado a la posteridad su célebre frase: «Dadme un punto de apoyo y moveré el mundo»
El rey le propuso entonces demostrar tal afirmación moviendo una gran galera anclada junto a la playa, que debía trasladar a tierra firme.
Mediante cuerdas, poleas y palancas, colocadas adecuadamente, y aplicando los resultados de sus experimentos, el sabio consiguió su propósito. Incluso el propio rey pudo realizar el «milagroso» experimento con sus propias manos.
El soberano cogió la cuerda, tiró de ella y comprobó cómo la proa de la nave se levantaba lentamente.
La multitud que observaba la extraordinaria hazaña prorrumpió en aclamaciones; Arquímedes recibió la felicitación del rey.
Se le atribuyen muchos descubrimientos: desde el principio que lleva su nombre hasta la medición del diámetro aparente del Sol y el principio de la palanca.
En este sentido, la frase que se le atribuye: «Dadme un punto de apoyo y moveré el mundo» es absolutamente cierta, porque, de hecho, es posible levantar un peso muy grande con muy poco esfuerzo haciendo fuerza en el extremo de una palanca muy larga y colocando el peso cerca del punto de apoyo.
El Tornillo de Arquímedes, o tornillo sin fin, es una máquina hidráulica utilizada en Egipto para el riego de los campos muy distantes del Nilo, y en España para bombear el agua de las minas.
Aunque algunos dudaron de la paternidad del sabio siracusano, los documentos papirológicos demuestran que esta máquina es posterior al siglo III a.C.
En uno de los frescos de Pompeya aparece un tornillo sin fin instalado horizontalmente y accionado por un pequeño esclavo.
Este instrumento, simple pero eficaz, se difundió ampliamente durante la Antigüedad, y todavía se utiliza en Egipto.

Arquímedes debe su fama a sus famosos inventos mecánicos, como las máquinas de guerra o el tornillo para elevar agua con el fin de irrigar los campos.
Esta máquina, llamada tornillo de Arquímedes, consiste en un cilindro dentro del cual rueda un helicoide (véase el dibujo superior). También son suyos los inventos de la rueda dentada y la polea móvil, aunque se cree que este tipo de inventos representaba para él sólo un juego.
► El principio de Arquímedes:
Pero, sin duda, el descubrimiento más célebre de Arquímedes es el relacionado con ll pérdida de peso que experimentan los cuerpos cuando se sumergen en un líquido.

En una ocasión, al mencionado rey Hierón le regalaron una corona de oro. Según cuentan, encargó a Arquímedes determinar si era de oro puro o contenía otros mi tales menos apreciados, como la plata.
Para solucionar el problema, era necesario hallar la densidad relativa de la corona, sin destruirla, y comparar este valor con el del densidad relativa del oro.
Arquímedes, si bien al principio no supo dar respuesta a la cuestión que se le planteaba, halló la solución de manera accidental, mientras tomaba un baño.
Observó que cuando su cuerpo se sumergía en la bañera, completamente llena, de agua se desbordaba.Se dio cuenta entonces de que el peso de un cuerpo sumergido en agua era inferior a la medida observada si se pesaba en el aire.
Obviamente, el agua ejercía una fuerza hacia arriba, que equilibraba, en parte, la fuerza de la gravedad.
Entonces Arquímedes realizó el experimento siguiente: tomó un recipiente completamente lleno de agua e introdujo en él una pieza de oro de peso análogo al de la corona; a continuación, pesó él agua que se desbordaba.
Después volvió a llenar de líquido al completo el recipiente, y sumergió la corona del rey, procediendo, igualmente, a registrar el peso del agua desbordada.
Arquímedes dedujo que la densidad relativa de la corona era igual al cociente entre su peso y su pérdida de peso cuando se la sumergía en agua; por lo tanto, tal magnitud podía determinarse pesando la corona primero en el aire y luego en el agua.
En el caso de que la corona fuera completamente de oro, el peso del agua desbordada en ambos casos debería ser el mismo, cosa que no ocurrió.
Las densidades de ambos cuerpos, por lo tanto, debían ser diferentes, por lo que la concluían estaba clara: el rey había sido engañado.
Los resultados que Arquímedes extrajo de este sencillo experimento pueden generalizarse a cualquier fluido: la fuerza ejercida por un fluido sobre un cuerpo sumergido total o parcialmente en él depende de la densidad del fluido y del volumen del cuerpo, pero no de la composición ni de la forma del objeto; este valor es equivalente en módulo al peso del fluido desalojado por dicho cuerpo.
Es el llamado «principio de Arquímedes», fundamento de la flotación de los cuerpos, tanto para medios líquidos como gaseosos.
Los resultados de esta experiencia fueron expuestos por el sabio en su libro Equilibrio de los cuerpos flotantes.
¿Por qué construyó máquinas de guerra?:
Vivió en los años de las guerras entre Roma y Cartago, por eso contribuyó activamente a la defensa de su ciudad asediada por las tropas romanas, al mando del cónsul Marcelo.
Para esta ocasión construyó unas máquinas de guerra que hicieron muy difícil a los romanos la conquista de la isla de Sicilia.
Se cuenta que logró quemar las naves romanas maniobrando desde lejos los terribles espejos ustorios, que funcionaban como lentes que concentraban los rayos del sol.
Las naves que lograban huir del rayo de fuego de sus espejos tenían que hacer frente a otro invento suyo: un artilugio que, tras elevarlas un poco en el aire, las estrellaba contra la costa escarpada.
Durante el asedio de Siracusa, Arquímedes, deseoso de salvar su ciudad, construyó también la catapulta múltiple, capaz de arrojar masas esféricas de un quintal de peso, y preparó proyectiles de largo alcance.
¿Cómo murió Arquímedes?:
Los testimonios que nos han quedado afirman que fue un hombre siempre inmerso en las lucubraciones matemáticas.
Hasta tal punto que cuando los romanos, ya vencedores, entraron en su casa, en el 212 a.C, y le conminaron a seguirles, él les pidió que esperaran a que acabase el problema de geometría que tenía entre manos, pero un soldado impaciente lo asesinó.

EN EL SITIO DE SIRACUSA
En el año 216, cuando Arquímedes tenía más de setenta años de edad, murió el tirano (rey) Hierón, que había sido su pariente.
Siracusa decidió aliarse con los cartagineses —era en el transcurso de la segunda guerra púnica— y le puso sitio un ejército romano al mando del cónsul Claudio Marcelo.Arquímedes era viejo y deseaba continuar tranquilamente con sus estudios.
Sus conciudadanos, empero, conociendo sus dotes intelectuales, se dirigieron a él para que colaborara en la defensa de la ciudad. Arquímedes, que siempre había sabido cumplir con sus deberes cívicos, accedió.
La tripulación de una de las naves sitiadoras que había osado acercarse a las fortificaciones, vio aparecer, con el despuntar del día, por encima de las murallas, una especie de monstruosa y enorme tenaza que aferró entre sus garras al navío, lo sacudió con fuerza y casi lo destruyó.
Era una máquina bélica proyectada por Arquímedes, que funcionaba sobre la base de palancas y poleas. Al mismo tiempo, desde las murallas y desde las fortificaciones comenzaron a caer sobre las otras naves ancladas a corta distancia, flechas y pesadas piedras lanzadas con catapultas, que destruían puentes y cascos, destrozaban los mástiles y daban muerte a los tripulantes.
Aprendió probablemente de su padre un sin fin de disciplinas matemáticas, para proseguir sus estudios en la escuela de Alejandría, Egipto.
En Egipto hizo su primer gran invento, la coclea, una especie de máquina que servía para elevar las aguas y regar ciertas regiones del Nilo, donde no
Llegaba el agua durante las inundaciones.
De vuelta a Siracusa, alternó inventos mecánicos con estudios de mecánica teórica y altas matemáticas.
Entre sus inventos cabe destacar numerosas máquinas de guerra, un  método para la determinación del peso específico de los cuerpos y un planetario mecánico.
método para la determinación del peso específico de los cuerpos y un planetario mecánico.
Su historia está llena de anécdotas y algunas de sus frases han pasado a la historia: Dame un punto de apoyo y moveré la Tierra, que resume el principio de la palanca, formulado por Arquímedes.
Según la tradición, Arquímedes es el tipo perfecto del gran matemático que el pueblo Concibe. Se olvidaba de comer cuando estaba ensimismado en La Matemática.
Su falta de atención por el vestido quedó de manifiesto cuando hizo su descubrimiento fundamental de que un cuerpo que flota pierde de peso una cantidad igual a la del líquido que desaloja (principio de Arquímedes) salió del baño, en el cual había hecho el descubrimiento al observar su propio cuerpo flotante, y corrió por las calles de Siracusa, completamente desnudo, gritando: Eureka,… eureka (lo encontré,… lo encontré).
Lo que había encontrado era la primera Ley de la Hidrostática.
Refiere la historia que un orfebre había adulterado el oro de una corona para Hierón II mezclándolo con plata, y el tirano, al sospechar el engaño, había planteado a Arquímedes el problema.
Cualquier estudiante sabe cómo se resuelve, mediante un simple experimento, y algunas fáciles cuentas aritméticas, basadas en el peso específico.
Arquímedes fue una especie de águila solitaria. Siendo joven había estudiado breve tiempo en Alejandría Egipto, donde contrajo dos amistades íntimas, Conan, un matemático de talento por quien Arquímedes tenía un alto concepto personal e intelectual, y Eratóstenes, también buen matemático.
Estos dos, particularmente Conan, parece que fueron los únicos hombres a quienes Arquímedes participó sus pensamientos seguro de ser comprendido.
Algunos de sus trabajos más complicados fueron comunicados por cartas a Canon. Más tarde, cuando Canon murió, Arquímede5 mantuvo correspondencia con Dositeo, un discípulo de Conan.
Sus publicaciones son obras cortas, especie de monografías.
De las espirales: genera la espiral, conocida como la espiral de Arquímedes, por movimientos.
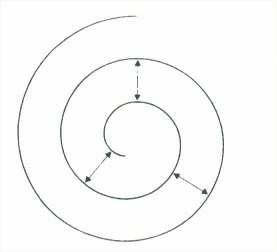
Es la curva que describe un punto que se mueve, con velocidad constante, sobre una recta que a su vez gira con velocidad constante. Combina dos movimientos, el circular uniforme de la semirrecta alrededor del origen y el rectilíneo uniforme del punto sobre la semirrecta.
Su ecuación en coordenadas polares es r=a.Þ donde r es la distancia al origen, a una constante y theta (Þ) es el ángulo girado.
Muy sorprendente para los matemáticos, fueron sus resultados sobre la espiral uniforme, recogidos en su libro "Sobre las espirales", en el que entre sus 28 proposiciones varias se refieren a las áreas de las espirales.
Resultados tan complejos como estos:
"El área barrida por el radio de la espiral en su primera revolución es la tercera parte del área del círculo cuyo radio es el radio final de esta revolución..."
"El área barrida por el radio en la segunda vuelta es 6 veces el área de la primera vuelta".
"El área barrida en la segunda revolución está en razón 7/12 con el círculo cuyo radio es la posición final del radio vector"
De la esfera y el cilindro: se dedica a La geometría y completa la obra de Euclides. Elabora una geometría del espacio con rigor. Relaciona áreas de distintas figuras. Busca una relación entre las áreas del cilindro y de La esfera.

Arquímedes partió de una semiesfera de radio R y colocó a su lado un cono recto y un cilindro circular recto, ambos con base de radio también R:
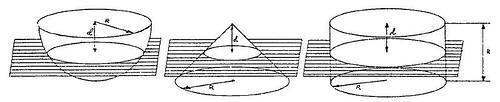
Cortó las tres figuras con un plano paralelo a la base del cilindro (que quedara a distancia d de la parte superior de las tres figuras) y estudió cómo serían las secciones que este plano crearía en cada una de las figuras:
Volumen cilindro = Volumen semiesfera + Volumen cono
![]()
![]()
![]()
El área lateral del cilindro es igual al área de la esfera inscripta.
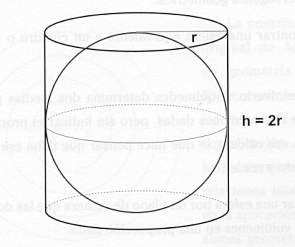
Arquímedes estaba tan orgulloso de este descubrimiento que mandó se inscribiera en su tumba: volumen de la esfera es 2/3 del cilindro.
De la cuadratura del círculo: vincula el problema de hallar un cuadrado de área igual área que La de un círculo.
Esto significa encontrar un segmento que tenga la longitud de la circunferencia. El problema depende de ir. No se puede hacer con regla y compás por ser ir trascendente, porque no se puede obtener como raíz de una ecuación algebraica.
Arquímedes da un procedimiento para determinar ir por sucesiones formadas por perímetros de polígonos regulares inscriptos y circunscriptos en una circunferencia.
Al dividir por el diámetro se obtienen sucesiones numéricas y éstas definen ir como elementos de separación. Así fijó el valor de Pi (entre 3 1/7 y 3 10/71.
De la parábola: en este libro plantea un procedimiento semejante al actual de integración para calcular el área de un recinto plano Limitado por un arco de parábola y una recta. Divide La región en triángulos y va calculando sus áreas hasta aproximarse al área buscada.
De las conoides y esferoides: trata las cuádricas de revolución. De Las 5 trata solo 3. El elipsoide haciendo girar una elipse, eL hiperboloide de 2 hojas, haciendo girar una parábola y el paraboloide haciendo girar una parábola.
Arenario: en este trabajo explica la diferencia entre un número finito y un número infinito. Se refiere a la cantidad de granitos de arene que entran en una semilla de amapolas y cuántas de éstas en el globo terráqueo. Como no los puede determinar establece el sistema de octavas:
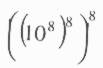
Con este procedimiento pensaba hallar un número para contar los granitos de arena.
Además encontró métodos para hallar las raíces cuadradas aproximadas, lo que muestra que se anticipó a la invención hecha por tos hindúes, respecto a las fracciones continuas periódicas.
En Aritmética sobrepasó extraordinariamente la incapacidad del método no científico griego de simbolizar los números al escribir o incluso escribir grandes números, e inventó un sistema de numeración capaz de tratar números tan grandes como se deseara.
En mecánica estableció algunos de los Postulados fundamentales, descubrió las leyes de la palanca, y aplicó sus principios mecánicos para calcular las áreas y centros de gravedad de diversas superficies planas y sólidos de diversas formas.
Creó toda la ciencia de la hidrostática, y la aplicó para encontrar las Posiciones de reposo y de equilibrio de cuerpos flotantes de diversos tipos.
A partir del siglo XIII se recuperó su obra en Europa Occidental, pero no fue hasta el XVI cuando los matemáticos volvieron a adquirir la suficiente capacidad para entenderla.
La vida de Arquímedes era tan tranquila como debe ser la de un matemático que ha hecho lo que él hizo.
Toda la acción y tragedia de vida quedan coronadas en su muerte.
En el año 212 a.C. estalló la segunda Guerra Púnica.
Roma y Cartago estaban en guerra, y Siracusa, la ciudad de Arquímedes tentadoramente situada cerca del camino de la flota romana. ¿Por qué no sitiarla? Eso hicieron los romanos.
Orgulloso de sí mismo, el jefe romano, Marcelo, estaba seguro de una rápida conquista.
Considerando su fama, esperaba que los tímidos ciudadanos Pusieran en sus manos la llave de la ciudad. Hierón II no lo hizo así.
Estaba bien preparado para la guerra y de una manera que el práctico Marcelo no podía soñar.
Los necios habitantes de Siracusa se entregaban a una fiesta religiosa en honor de Artemisa.
La guerra y La religión siempre han dado lugar a un peligroso cocktail; sorprendidos en la fiesta, Marcelo hizo una carnicería.
La primera noticia que tuvo Arquímedes de que la ciudad había sido tomada fue la sombra de un soldado romano que se proyectaba sobre sus dibujos en la arena.
Un relato dice que el soldado, al pisar Los dibujos, dio Lugar a que Arquímedes exclamara excitadamente: No borres mis círculos.
Otros afirman que Arquímedes se negó a obedecer la orden de un soldado, para que le acompañara a presencia de Marcelo, hasta que hubiera resuelto su problema.
De todos modos Lo cierto es que el irritado soldado desenvainó su sable y dio muerte al inerme geómetra que a La sazón tenía 70 años.
Así murió Arquímedes en Siracusa cuando Los romanos la capturaron en 212 a.C.
DESCRIPCIÓN DEL PRINCIPIO DE ARQUÍMEDES:
Figura Abajo: Un cuerpo sumergido en un líquido pierde una parte de su peso igual al peso del volumen del líquido desalojado. Obsérvese como varia el brazo de la balanza cuando la piedra está sumergida.
 Existe en física un importante principio que fue descubierto por Arquímedes, el más grande físico y matemático de la Antigüedad.
Existe en física un importante principio que fue descubierto por Arquímedes, el más grande físico y matemático de la Antigüedad.
Dicho principio dice que un cuerpo sumergido en un líquido recibe un empuje hacia arriba igual al peso del líquido desalojado.
Si, por ejemplo, sumergimos un huevo, que puede tener un volumen de 60 centímetros cúbicos, en el agua, recibirá un empuje hacia arriba igual al peso de 60 centímetros cúbicos de agua; es decir, 60 gramos.
Y si el huevo pesa 50 gramos, el empuje resultante será de 60 — 50 = 10 gramos, que es suficiente para mantenerlo a flote; el peso específico del huevo es menor que el del agua.
Si en vez de un huevo de gallina se hubiese tratado de otro de igual forma y volumen, pero de plomo, es evidente que se hubiera ido al fondo, ya que el empuje del agua hubiera sido mucho menor que su peso.
En este hecho se basa un modo muy simple para saber si un huevo es o no fresco.
El huevo fresco tiene un peso específico ligeramente superior al agua, y por esto se sumerge; el que no es fresco, en el cual ha entrado aire o se han producido gases de descomposición, tiene densidad menor que la del agua, y flota.
Del principio de Arquímedes poseemos numerosísimos e importantes ejemplos y aplicaciones. Las naves, también de hierro, flotan porque su peso total es menor que el peso del volumen de agua que desalojan.
En los submarinos se necesita introducir agua en el momento de la inmersión, a fin de que aumente el peso total del mismo y así supere al del agua desalojada.
Por el mismo motivo, los globos y dirigibles se mantienen en el aire: se llenan de gas (hidrógeno, helio) cuya densidad es menor que la del aire.
Pero hay más todavía. Esto, que sucede para los cuerpos sólidos de forma y volumen bien definidos, ocurre también para las masas de líquidos y gases que presentan en su seno zonas o partes de distintas densidades.
¿Por qué el humo sale y las chimeneas "tiran"?. El humo y los gases de la combustión son más calientes y por lo tanto menos densos que el aire circundante; por esto son empujados hacia arriba por el aire frío.
Si el humo sale por una chimenea, se puede calcular con exactitud el empuje o presión (depresión, para ser más correctos) al pie de la chimenea midiendo la temperatura del humo y del aire ambiente.
Así también, al verter agua fría en una vasija donde hay agua caliente, el agua vertida "cae" al fondo, quedando situada debajo de la caliente.
Del mismo modo se explican dos importantísimos fenómenos, cuales son los de las corrientes marinas y de los vientos.
Se trata de masas fluidas, de agua o aire, puestas en movimiento debido a su diferencia de densidad, respecto a las masas cercanas, cuando son calentadas por la irradiación solar.
► LA TRÁGICA MUERTE:
El asedio romano continuó con la implacabilidad con que los romanos procedían en tales casos.
Durante cuatro años pudo defenderse Siracusa, hasta que en el año 212, el día de la fiesta de la diosa Artemisa, las tropas sitiadoras lograron entrar en la ciudad y la saquearon.
Durante estas horas trágicas, varios soldados romanos penetraron en la casa de Arquímedes.
El sabio hallábase sumido en sus cálculos geométricos y no oyó siquiera la gritería, el fragor de las armas y el pataleo de los caballos que llegaban de afuera.
Uno de los soldados llegó hasta la sala donde el sabio trabajaba, ajeno a la tremenda lucha que se libraba en la ciudad.
Se dice que el intruso experimentó desconfianza- hacia el anciano, absorto en su trabajo, y supuso que su actitud debía ocultar algún ardid.
Arquímedes había trazado algunas figuras geométricas en el piso, y al ver las sandalias del insólito visitante demasiado cercanas a sus dibujos, formuló una advertencia pidiéndole que tuviera cuidado de no pisarlos.
El soldado, que estaba contemplando con codicia los instrumentos, atribuyéndoles valor considerable, levantó su espada y asesinó fríamente al anciano. Éste tenia entonces setenta y cinco años.
Curiosidad: Se le ha dado el nombre de Arquímedes a un círculo de montañas lunares de unos 80 Km. de diámetro.
Fuente Consultada:
Gran Enciclopedia
Universal Espasa Calpe Tomo 4 Entrada: Arquímedes
Arquímedes y La Palanca Paul Strathern





